Difference between revisions of "Projects:fMRIClustering"
m (Algorithm:MIT:fMRI Clustering moved to Projects:fMRIClustering) |
|||
| Line 1: | Line 1: | ||
| − | Back to [[NA-MIC_Collaborations|NA- | + | Back to [[NA-MIC_Collaborations|NA-MIC Collaborations]], [[Algorithm:MIT|MIT Algorithms]] |
| + | __NOTOC__ | ||
= fMRI Clustering = | = fMRI Clustering = | ||
| Line 77: | Line 78: | ||
= Key Investigators = | = Key Investigators = | ||
| − | * MIT: Danial Lashkari, Polina Golland, Nancy Kanwisher | + | * MIT Algorithms: Danial Lashkari, Polina Golland, Nancy Kanwisher |
= Publications = | = Publications = | ||
| Line 83: | Line 84: | ||
''In print'' | ''In print'' | ||
| − | * | + | * [http://www.na-mic.org/Special:Publications?text=Projects%3AfMRIClustering&submit=Search&words=all&title=checked&keywords=checked&authors=checked&abstract=checked&sponsors=checked&searchbytag=checked| NA-MIC Publications Database] |
''In press'' | ''In press'' | ||
| − | * D. Lashkari, P. Golland. Convex Clustering with Exemplar-Based Models. In NIPS: Advances in Neural Information Processing Systems, 2007. | + | * D. Lashkari, P. Golland. Convex Clustering with Exemplar-Based Models. In NIPS: Advances in Neural Information Processing Systems, 2007. |
| − | |||
| − | |||
Revision as of 20:34, 22 December 2007
Home < Projects:fMRIClusteringBack to NA-MIC Collaborations, MIT Algorithms
fMRI Clustering
One of the major goals in analysis of fMRI data is the detection of networks in the brain with similar functional behavior. A wide variety of methods including hypothesis-driven statistical tests, unsupervised learning methods such as PCA and ICA, and different clustering algorithms have been employed to find these networks. This project aims to particularly study application of model-based clustering algorithms in identification of functional connectivity in the brain.
Description
Generative Model for Functional Connectivity
In the classical functional connectivity analysis, networks of interest are defined based on correlation with the mean time course of a user-selected `seed' region. Further, the user has to also specify a subject-specific threshold at which correlation values are deemed significant. In this project, we simultaneously estimate the optimal representative time courses that summarize the fMRI data well and the partition of the volume into a set of disjoint regions that are best explained by these representative time courses. This approach to functional connectivity analysis offers two advantages. First, is removes the sensitivity of the analysis to the details of the seed selection. Second, it substantially simplifies group analysis by eliminating the need for the subject-specific threshold. Our experimental results indicate that the functional segmentation provides a robust, anatomically meaningful and consistent model for functional connectivity in fMRI.
We formulate the problem of characterizing connectivity as a partition of voxels into subsets that are well characterized by a certain number of representative hypotheses, or time courses, based on the similarity of their time courses to each hypothesis. We model the fMRI signal at each voxel as generated by a mixture of Gaussian distributions whose centers are the desired representative time courses. Using the EM algorithm to solve the corresponding model-fitting problem, we alternatively estimate the representative time courses and cluster assignments to improve our random initialization.
Experimental Results
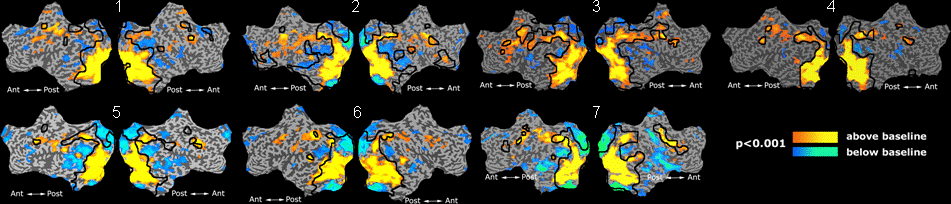
We used data from 7 subjects with a diverse set of visual experiments including localizer, morphing, rest, internal tasks, and movie. The functional scans were pre-processed for motion artifacts, manually aligned into the Talairach coordinate system, detrended (removing linear trends in the baseline activation) and smoothed (8mm kernel).
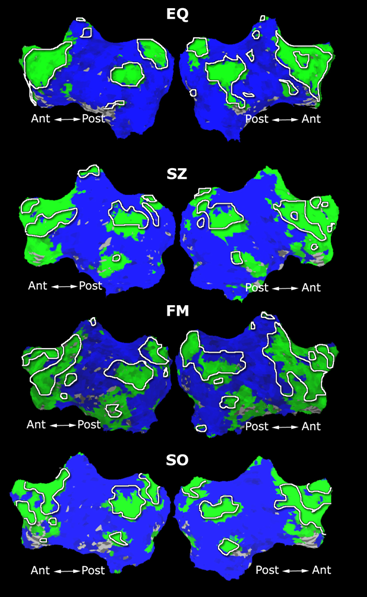
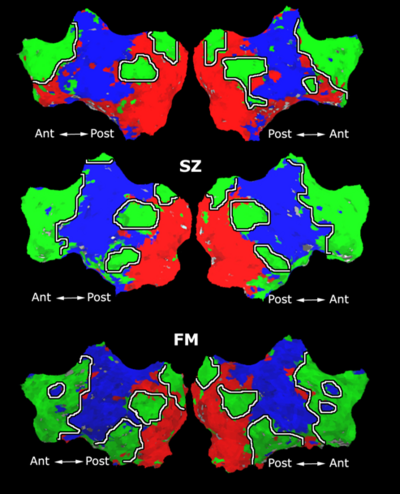
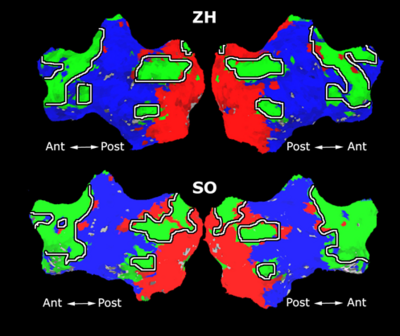
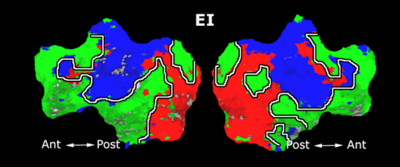
Fig. 1 shows the 2-system partition extracted in each subject independently of all others. It also displays the boundaries of the intrinsic system determined through the traditional seed selection, showing good agreement between the two partitions. Fig. 2 presents the results of further clustering the stimulus-driven cluster into two clusters independently for each subject.
| Fig 1. 2-System Parcelation. Results for all 7 subjects. | Fig 2. 3-System Parcelation. Results for all 7 subjects. |
|---|---|
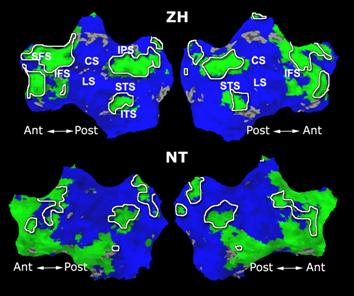
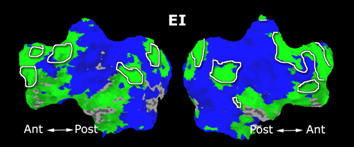
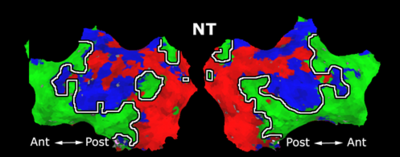
Fig.3 presents the group average of the subject-specific 2-system maps. Color shading shows the proportion of subjects whose clustering agreed with the majority label. Fig. 4 shows the group average of a further parcelation of the intrinsic system, i.e., one of two clusters associated with the non-stimulus-driven regions. In order to present a validation of the method, we compare these results with the conventional scheme for detection of visually responsive areas. In Fig. 5, color shows the statistical parametric map while solid lines indicate the boundaries of the visual system obtained through clustering. The result illustrate the agreement between the two methods.
| Fig 3. 2-System Parcellation. Group-wise result. | |
|---|---|
|
|
Clustering Study of Domain Specificity in High Level Visual Cortex
As a more specific application of clustering model-based algorithms, we are currently investigating devising clustering algorithms for detection of functional connectivity in high-level visual cortex. It is suggested that there are regions in the visual cortex with high selectivity to certain categories of visual stimuli. Currently, the conventional method for detection of these methods is based on statistical tests comparing response of each voxel in the brain to different visual categories to see if it shows considerably higher activation to one category. For example, the well-known FFA (Fusiform Face Area) is the set of voxels which show high activation to faces when compared to objects. We are working on using the clustering the visual cortex as a means to make this analysis automatic and further discover new structures in the high-level visual cortex.
Key Investigators
- MIT Algorithms: Danial Lashkari, Polina Golland, Nancy Kanwisher
Publications
In print
In press
- D. Lashkari, P. Golland. Convex Clustering with Exemplar-Based Models. In NIPS: Advances in Neural Information Processing Systems, 2007.