Difference between revisions of "Projects:RegistrationRegularization"
| Line 1: | Line 1: | ||
Back to [[NA-MIC_Internal_Collaborations:StructuralImageAnalysis|NA-MIC Collaborations]], [[Algorithm:MIT|MIT Algorithms]] | Back to [[NA-MIC_Internal_Collaborations:StructuralImageAnalysis|NA-MIC Collaborations]], [[Algorithm:MIT|MIT Algorithms]] | ||
| − | We propose a unified framework for computing atlases from manually labeled data sets at various degrees of “sharpness” and the joint registration and segmentation of a new brain with these atlases. In non-rigid registration, the tradeoff between warp regularization and image fidelity is typically set empirically. In segmentation, this leads to a probabilistic atlas of arbitrary “sharpness”: weak regularization results in well-aligned training images, producing a “sharp” atlas; strong regularization yields a “blurry” atlas. We study the effects of this tradeoff in the context of cortical surface parcellation, but the framework applies to volume registration as well. | + | We propose a unified framework for computing atlases from manually labeled data sets at various degrees of “sharpness” and the joint registration and segmentation of a new brain with these atlases. In non-rigid registration, the tradeoff between warp regularization and image fidelity is typically set empirically. In segmentation, this leads to a probabilistic atlas of arbitrary “sharpness”: weak regularization results in well-aligned training images, producing a “sharp” atlas; strong regularization yields a “blurry” atlas. We study the effects of this tradeoff in the context of cortical surface parcellation, but the framework applies to volume registration as well. This is an important question because of the increasingly availability of atlases in public databases and the development of registration algorithms separate from the atlas construction process. |
= Description = | = Description = | ||
| + | We employ a generative model for the joint registration and segmentation of images. The atlas construction process arises naturally as estimation of the model parameters. This framework allows the computation of unbiased atlases from manually | ||
| + | labeled data at various degrees of "sharpness", as well as the joint registration and segmentation of a novel brain in a consistent manner. | ||
| + | |||
In image registration, one usually optimizes the objective function with two parts. The first term is the similarity between images. The second term regularizes the warp. The smoothness parameter C that weights the second term determines the tradeoff between the similarity measure and the regularization. | In image registration, one usually optimizes the objective function with two parts. The first term is the similarity between images. The second term regularizes the warp. The smoothness parameter C that weights the second term determines the tradeoff between the similarity measure and the regularization. | ||
| Line 14: | Line 17: | ||
We compare three special cases of our framework, namely: | We compare three special cases of our framework, namely: | ||
| − | (1) Progressive registration of a new brain to increasingly “sharp” atlases using increasingly | + | (1) Progressive registration of a new brain to increasingly “sharp” atlases using increasingly flexible warps, by initializing each registration stage with the optimal warps from a “blurrier” atlas. We call this multiple atlases, multiple warp scales (MAMS). |
| − | flexible warps, by initializing each registration stage with the optimal warps from | ||
| − | a “blurrier” atlas. We call this multiple atlases, multiple warp scales (MAMS). | ||
| − | (2) Progressive registration to a single atlas with increasingly | + | (2) Progressive registration to a single atlas with increasingly flexible warps. We call this single atlas, multiple warp scales (SAMS). |
| − | flexible warps. We call this single atlas, multiple warp scales (SAMS). | ||
(3) Registration to a single atlas with fixed constrained warps. We call this single atlas, single warp scale (SASS). | (3) Registration to a single atlas with fixed constrained warps. We call this single atlas, single warp scale (SASS). | ||
| Line 26: | Line 26: | ||
[[Image:JointRegSeg.png|center|400px|]] | [[Image:JointRegSeg.png|center|400px|]] | ||
| − | We use dice as the measure of segmentation quality. From the graph below, we note that the optimal parcellation algorithm in all three cases yield a statistically significant improvement over a state-of-the-art benchmark parcellation algorithm [1,2]. The optimal algorithms correspond to a unique balance between atlas “sharpness” and warp regularization. Our experiments show that the optimal parameter values that correspond to this balance can be determined using leave-out experiments. This optimal value seems to be robust across subjects, and the same for both co-registration of the training data and registration of a new subject. This suggests that a single atlas at an optimal sharpness is sufficient to achieve the best segmentation results. | + | We use dice as the measure of segmentation quality. From the graph below, we note that the optimal parcellation algorithm in all three cases yield a statistically significant improvement over a state-of-the-art benchmark parcellation algorithm [1,2]. The optimal algorithms correspond to a unique balance between atlas “sharpness” and warp regularization. Our experiments show that the optimal parameter values that correspond to this balance can be determined using leave-out experiments. This optimal value seems to be robust across subjects, and the same for both co-registration of the training data and registration of a new subject. This suggests that a single atlas at an optimal sharpness is sufficient to achieve the best segmentation results. Furthermore, the optimal atlas sharpness and warp smoothness can be determined by probing the segmentation performance on available training data. Our experiments also suggest that segmentation accuracy is tolerant up to a small mismatch between atlas sharpness and warp smoothness. |
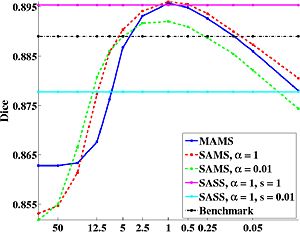
[[Image:AvgResults.jpg|thumb|center|300px|Plot of Dice as a function of the warp smoothness S. Note that S is on a log scale. <math>\alpha</math> corresponds to the sharpness of the atlas used.]] | [[Image:AvgResults.jpg|thumb|center|300px|Plot of Dice as a function of the warp smoothness S. Note that S is on a log scale. <math>\alpha</math> corresponds to the sharpness of the atlas used.]] | ||
| + | |||
= Key Investigators = | = Key Investigators = | ||
Revision as of 17:28, 19 May 2008
Home < Projects:RegistrationRegularizationBack to NA-MIC Collaborations, MIT Algorithms
We propose a unified framework for computing atlases from manually labeled data sets at various degrees of “sharpness” and the joint registration and segmentation of a new brain with these atlases. In non-rigid registration, the tradeoff between warp regularization and image fidelity is typically set empirically. In segmentation, this leads to a probabilistic atlas of arbitrary “sharpness”: weak regularization results in well-aligned training images, producing a “sharp” atlas; strong regularization yields a “blurry” atlas. We study the effects of this tradeoff in the context of cortical surface parcellation, but the framework applies to volume registration as well. This is an important question because of the increasingly availability of atlases in public databases and the development of registration algorithms separate from the atlas construction process.
Description
We employ a generative model for the joint registration and segmentation of images. The atlas construction process arises naturally as estimation of the model parameters. This framework allows the computation of unbiased atlases from manually labeled data at various degrees of "sharpness", as well as the joint registration and segmentation of a novel brain in a consistent manner.
In image registration, one usually optimizes the objective function with two parts. The first term is the similarity between images. The second term regularizes the warp. The smoothness parameter C that weights the second term determines the tradeoff between the similarity measure and the regularization.
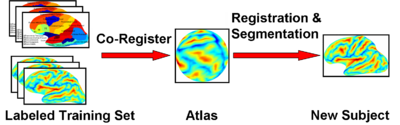
In Atlas-Based Segmentation, one is given a set of labeled training images. The training images are co-registered to a common space. An atlas that summarizes the information between the image features and the labels is computed in this common space. This atlas is used to segment and normalize a new image.
In this study, we propose a unified framework for computing atlases from manually labeled data at various degrees of “sharpness” and the joint registration-segmentation of a new brain with these atlases. Using this framework, we investigate the tradeoff between warp regularization and image fidelity, i.e. the smoothness of the new subject warp and the srapness of the atlas.
We compare three special cases of our framework, namely:
(1) Progressive registration of a new brain to increasingly “sharp” atlases using increasingly flexible warps, by initializing each registration stage with the optimal warps from a “blurrier” atlas. We call this multiple atlases, multiple warp scales (MAMS).
(2) Progressive registration to a single atlas with increasingly flexible warps. We call this single atlas, multiple warp scales (SAMS).
(3) Registration to a single atlas with fixed constrained warps. We call this single atlas, single warp scale (SASS).
We use dice as the measure of segmentation quality. From the graph below, we note that the optimal parcellation algorithm in all three cases yield a statistically significant improvement over a state-of-the-art benchmark parcellation algorithm [1,2]. The optimal algorithms correspond to a unique balance between atlas “sharpness” and warp regularization. Our experiments show that the optimal parameter values that correspond to this balance can be determined using leave-out experiments. This optimal value seems to be robust across subjects, and the same for both co-registration of the training data and registration of a new subject. This suggests that a single atlas at an optimal sharpness is sufficient to achieve the best segmentation results. Furthermore, the optimal atlas sharpness and warp smoothness can be determined by probing the segmentation performance on available training data. Our experiments also suggest that segmentation accuracy is tolerant up to a small mismatch between atlas sharpness and warp smoothness.
Key Investigators
- MIT Algorithms: [| B.T. Thomas Yeo], Mert Sabuncu, Rahul Desikan, Bruce Fischl, Polina Golland
Publications
In Press
- B.T.T. Yeo, M.R. Sabuncu, R. Desikan, B. Fischl, P. Golland. Effects of Registration Regularization and Atlas Sharpness on Segmentation Accuracy. Accepted to Medical Image Analysis, 2008.
In Print