Projects:LearningRegistrationCostFunctions

Back to NA-MIC Collaborations, MIT Algorithms

We present a framework for learning registration cost functions. In medical image analysis, registration is rarely the final goal, but instead the resulting alignment is used in other tasks, such as image segmentation or group analysis. The parameters of the registration cost function -- for example, the tradeoff between the image similarity and regularization terms -- are typically determined manually through inspection of the image alignment and then fixed for all applications. However, it is unclear that the same parameters are optimal for different applications. In this paper, we propose a principled approach to leveraging the application context to effectively regularize the ill-posed problem of image registration. Our method learns the parameters of any smooth family of registration cost functions with respect to a specific task.

Description

Our key idea is to introduce a second layer of optimization over and above the usual registration. This second layer of optimization traverses the space of local minima, selecting registration parameters that result in good registration local minima as measured by the performance of the specific application in a training data set. The training data provides additional information not present in a test image, allowing the task-specific cost function to be evaluated during training. For example, if the task is segmentation, we assume the existence of a training data set with ground truth segmentation and a smooth cost function that evaluates segmentation accuracy.

If the registration cost function employs a single parameter, then the optimal parameter value can be found by exhaustive search. With multiple parameters, exhaustive search is not possible. Here, we demonstrate the optimization of thousands of parameters by gradient descent on the space of local minima, selecting registration parameters that result in good registration local minima as measured by the task-specific cost function in the training data set.

Our formulation is therefore related to the use of continuation methods in computing the entire path of solutions of learning problems (e.g., SVM or Lasso) as a function of a single regularization parameter. Because we deal with multiple (thousands of) parameters, it is impossible for us to compute a solution manifold. Instead, we trace a path within the solution manifold that improves the task-specific cost function. Furthermore, the registration cost function is not convex (unlike SVM and Lasso), resulting in several theoretical and practical challenges that we have to overcome, some of which we leave for future work.

Experimental Results

We instantiate the framework for the alignment of hidden labels whose extent is not necessarily well-predicted by local image features. We apply the resulting algorithm to localize cytoarchitectural and functional regions based only on macroanatomical cortical folding information and achieve state-of-the-art localization results in both histological and functional Magnetic Re

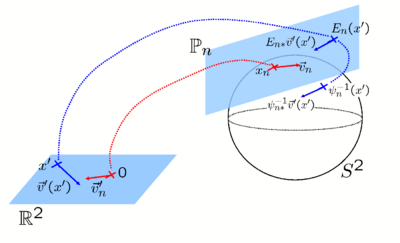
We use two sets of experiments to compare the accuracy of Spherical Demons and FreeSurfer [1]. The FreeSurfer registration algorithm uses the same similarity measure as Spherical Demons, but penalizes for metric and areal distortion. Its runtime is more than an hour while our runtime is less than 5 minutes.

(1) Parcellation of In-Vivo Cortical Surfaces

We consider a set of 39 left and right cortical surface models extracted from in-vivo MRI. Each surface is spherically parameterized and represented as a spherical image with geometric features at each vertex (e.g., sulcal depth and curvature). Both hemispheres are manually parcellated by a neuroanatomist into 35 major sulci and gyri. We validate our algorithm in the context of automatic cortical parcellation.

We co-register all 39 spherical images of cortical geometry with Spherical Demons by iteratively building an atlas and registering the surfaces to the atlas. The atlas consists of the mean and variance of cortical geometry. We then perform cross-validation parcellation 4 times, by leaving out subjects 1 to 10, training a classifier using the remaining subjects, and using it to classify subjects 1 to 10. We repeat with subjects 11-20, 21-30 and 31-39. We also perform registration and cross-validation with the FreeSurfer algorithm [1] using the same features and parcellation algorithm. Once again, the atlas consists of the mean and variance of cortical geometry.

The average Dice measure (defined as the ratio of cortical surface area with correct labels to the total surface area averaged over the test set) on the left hemisphere is 88.9 for FreeSurfer and 89.6 for Spherical Demons. While the improvement is not big, the difference is statistically significant for a one-sided t-test with the Dice measure of each subject treated as an independent sample (p = 2e-6). On the right hemisphere, FreeSurfer obtains a Dice of 88.8 and Spherical Demons achieves 89.1. Here, the improvement is smaller, but still statistically significant (p = 0.01).

Left Medial

Left Lateral

Right Lateral

Right Medial

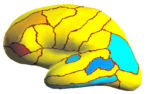
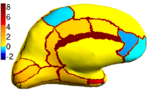
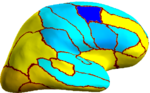
Because the average Dice can be deceiving by suppressing small structures, we analyze the segmentation accuracy per structure. On the left (right) hemisphere, the segmentations of 16 (8) structures are statistically significantly improved by Spherical Demons with respect to FreeSurfer, while no structure got worse (FDR = 0.05). The above figure shows the percentage improvement of individual structures. Parcellation results suggest that our registration is at least as accurate as FreeSurfer.

(2) Brodmann Areas Localization on Ex-vivo Cortical Surfaces

In this experiment, we evaluate the registration accuracy on ten human brains analyzed histologically postmortem. The histological sections were aligned to postmortem MR with nonlinear warps to build a 3D volume. Eight manually labeled Brodmann areas from histology were sampled onto each hemispheric surface model and sampling errors were manually corrected. Brodmann areas are cyto-architectonically defined regions closely related to cortical function.

It has been shown that nonlinear surface registration of cortical folds can significantly improve Brodmann area overlap across different subjects. Registering the ex-vivo surfaces is more difficult than in-vivo surfaces because the reconstructed volumes are extremely noisy, resulting in noisy geometric features.

We co-register the ten surfaces to each other by iteratively building an atlas and registering the surfaces to the atlas. We compute the average distance between the boundaries of the Brodmann areas for each pair of registered subjects. We perform a permutation test to test for statistical significance. Spherical Demons improves the alignment of 5 (2) Brodmann areas on the left (right) hemisphere (FDR = 0.05) compared with FreeSurfer and no structure gets worse. These results suggest that the Spherical Demons algorithm is at least as accurate as FreeSurfer in aligning Brodmann areas.

Code

Matlab code is currently available at http://yeoyeo02.googlepages.com/sphericaldemonsrelease

[1] B. Fischl, M. Sereno, R. Tootell, and A. Dale. High-resolution Intersubject Averaging and a Coordinate System for the Cortical Surface. Human Brain Mapping, 8(4):272–284, 1999.

[2] J. Thirion. Image Matching as a Diffusion Process: an Analogy with Maxwell’s Demons. Medical Image Analysis, 2(3):243–260, 1998.

[3] T. Vercauteren, X. Pennec, A. Perchant, and N. Ayache. Non-parametric Diffeomorphic Image Registration with the Demons Registration. In Proceedings of the International Conference on Medical Image Computing and Computer Assisted Intervention (MICCAI), volume 4792 of LNCS, pages 319–326, 2007.

Key Investigators

• MIT: [| B.T. Thomas Yeo], Mert Sabuncu, Tom Vercauteren, Nicholas Ayache, Bruce Fischl, Polina Golland

Publications

In Print

• NA-MIC Publications Database