Projects:LocalStatisticalAnalysisViaPermutationTests

Back to NA-MIC Collaborations, UNC Algorithms, Utah Algorithms

Local Statistical Analysis via Permutation Tests

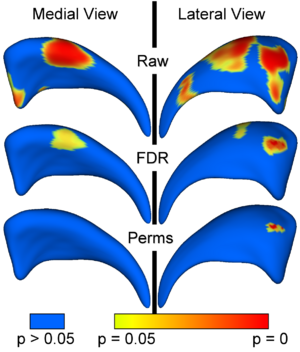
In our statistical framework, group differences between groups of surfaces are computed locally for every surface point using the standard robust Hotelling T^2 two sample metric. Statistical p-values, both raw and corrected for multiple comparisons, result in significance maps. Additional visualization of the group tests are provided via mean difference magnitude and vector maps, as well as maps of the group covariance information.

Description

The local shape analysis involves testing from a few to many thousands of hypothesis (one per surface ele- ment) for statistically significant effects. It is thus important to control for the multiple testing problem, and the most common measure of multiple false positives is the familywise error rate (FWER). The multiple testing problem has been an active area of research in the functional neuroimaging community. One of the widely used methods in the analysis of neuroimaging data makes inferences based on the maximum distribution. In our work, we are employing non-parametric permutation tests to estimate uniformly sensitive extrema distributions. The correction method is based on computing first the local p-values using permutation tests. The minimum of these p-values across the surface is then computed for every permutation. The appropriate corrected p-value at level α can then be obtained by the computing the value at the α-quantile in the histogram of these minimum values. Using the minimum statistic of the p-values, this method correctly controls for the FWER, or the false positives, but no control of the false negatives is provided. The resulting corrected local significance values can thus be regarded as pessimistic estimates akin to a simple Bonferroni correctection.

Additionally to the non-parametric permutation correction, we have also implemented and applied a False Discovery Rate Estimation (FDR) method. The innovation of this procedure is that it controls the expected proportion of false positives only among those tests for which a local significance has been detected. The FDR method thus allows an expected proportion (usually 5%) of the FDR corrected significance values to be falsely positive. The correction using FDR provides an interpretable and adaptive criterion with higher power than the non-parametric permutation tests. FDR thus results in a less conservative estimate of the false-negatives.

This framework has now been extended to include subject variables, such as gender, age and clinical scores into the previous pure group difference computation. This is done by first computing a Generalized Linear Model, followed by a MANCOVA analysis and p-value computation and correction via the same permutation approach mentioned above. Current work involves seamless integration of this MANCOVA tool into the shape analysis toolset, as well as development of an appropriate test dataset with know ground truth. Furthermore, the MANCOVA based testing framework contains facilities for z-score testing and correlation testing

Key Investigators

• UNC Algorithms: Martin Styner, Ipek Oguz, Marc Niethammer, Marc Macenko, Beatriz Paniagua, Christine Shun Xu, Hongtu Zhu
• Utah Algorithms: Guido Gerig

Publications

In Print

• NA-MIC Publications Database

• S. Olmos, M. Bossa, M. Styner: PCA-based filtering for hypothesis testing on hippocampus shape differences between schizophrenics and normals. Medical Image Understanding and Analysis 2005, Bristol, pp. 167-170.

Links

• ITK statistical analysis using non-parametric permutation analysis and false discovery rate

Project Week Results: Jun 2006