Difference between revisions of "Projects:LearningRegistrationCostFunctions"
(Created page with ' Back to NA-MIC Collaborations, MIT Algorithms We present the fast Spherical Demons algorithm for re…') |
|||
| (76 intermediate revisions by 6 users not shown) | |||
| Line 1: | Line 1: | ||
| − | Back to [[NA-MIC_Internal_Collaborations:StructuralImageAnalysis|NA-MIC Collaborations]], [[Algorithm:MIT|MIT Algorithms]] | + | Back to [[NA-MIC_Internal_Collaborations:StructuralImageAnalysis|NA-MIC Collaborations]], [[Algorithm:MIT|MIT Algorithms]], [[Algorithm:MGH|MGH Algorithms]] |
| + | __NOTOC__ | ||
| + | = Learning Task-Optimal Registration Cost Functions = | ||
| − | We present | + | We present a framework for learning the parameters of registration cost functions. The parameters of the registration cost function -- for example, the tradeoff between the image similarity and regularization terms -- are typically determined manually through inspection of the image alignment and then fixed for all applications. We propose a principled approach to learn these parameters with respect to particular applications. |
| − | |||
| − | |||
| − | |||
| − | |||
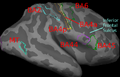
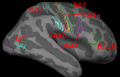
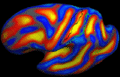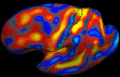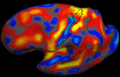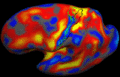
| − | + | Image registration is ambiguous. For example, the figures below show two subjects with Brodmann areas overlaid on their cortical folding patterns. Brodmann areas are parcellation of the cortex based on the cellular architecture of the cortex. Here, we see that perfectly aligning the inferior frontal sulcus will misalign the superior end of BA44 (Broca's language area). If our goal is segment sulci and gyri, perfectly alignment of the cortical folding pattern is ideal. But it is unclear whether perfectly aligning cortical folds is optimal for localizing Brodmann areas. Here, we show that by taking into account the end-goal of registration, we not only improve the application performance but also potentially eliminate ambiguities in image registration. | |
| − | |||
| − | |||
| − | + | <gallery> | |
| + | Image:to.rh.pm1696.BAsALL.lat.cropped.caption.png | ||
| + | Image:to.rh.pm20784.BAsALL.lat.cropped.caption.png | ||
| + | </gallery> | ||
| − | + | = Description = | |
| − | |||
| − | = | ||
| − | |||
| − | + | The key idea is to introduce a second layer of optimization over and above the usual registration. This second layer of optimization traverses the space of local minima, selecting registration parameters that result in good registration local minima as measured by the performance of the specific application in a training data set. The training data provides additional information not present in a test image, allowing the task-specific cost function to be evaluated during training. For example, if the task is segmentation, we assume the existence of a training data set with ground truth segmentation and a smooth cost function that evaluates segmentation accuracy. This segmentation accuracy is used as a proxy to evaluate registration accuracy. | |
| − | + | If the registration cost function employs a single parameter, then the optimal parameter value can be found by exhaustive search. With multiple parameters, exhaustive search is not possible. Here, we demonstrate the optimization of thousands of parameters by gradient descent on the space of local minima, selecting registration parameters that result in good registration local minima as measured by the task-specific cost function in the training data set. | |
| − | + | Our formulation is related to the use of continuation methods in computing the entire path of solutions of learning problems (e.g., SVM or Lasso) as a function of a single regularization parameter. Because we deal with multiple (thousands of) parameters, it is impossible for us to compute a solution manifold. Instead, we trace a path within the solution manifold that improves the task-specific cost function. | |
| − | |||
| + | Another advantage of our approach is that we do not require ground truth deformations. As suggested in the example above, the concept of “ground truth deformations” may not always be well-defined, since the optimal registration may depend on the application at hand. In contrast, our approach avoids the need for ground truth deformations by focusing on the application performance, where ground truth (e.g., via segmentation labels) is better defined. | ||
| − | + | == Experimental Results == | |
| − | |||
| − | + | We instantiate the framework for the alignment of hidden labels whose extents are not necessarily well-predicted by local image features. We consider the generic weighted Sum of Squared Differences (wSSD) cost function and estimate either (1) the optimal weights or (2) cortical folding template for localizing cytoarchitectural and functional regions based only on macroanatomical cortical folding information. We demonstrate state-of-the-art localization results in both histological and fMRI data sets. | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | == (1) Localizing Brodmann Areas Using Cortical Folding == | |
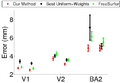
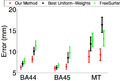
| − | + | In this experiment, we estimate the optimal template in the wSSD cost function for localizing Brodmann areas in 10 histologically-analyzed subjects. We compare 3 algorithms: task-optimal template (red), FreeSurfer (green) [1] and optimal uniform weights of the wSSD (black). The optimal uniform weights of the wSSD are found by setting all the weights to a single value and performing an exhaustive search of the weights. We see in the figure below, that task-optimal framework achieves the lowest localization errors. | |
| − | of | ||
| − | + | <gallery> | |
| + | Image:to.Presentation.mean2.V1V2BA2.png | ||
| + | Image:to.Presentation.mean2.BA44BA45MT.png | ||
| + | </gallery> | ||
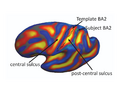
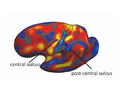
| − | In this | + | == (1b) Interpreting Task-Optimal Template Estimation == |
| + | Fig(a) shows the initial cortical geometry of a template subject with its corresponding BA2 in black outline. In this particular subject, the postcentral sulcus is more prominent than the central sulcus. Fig(b) shows the cortical geometry of a test subject together with its BA2. In this subject, the central sulcus is more prominent than the postcentral sulcus. Consequently, in the uniform-weights method, the central sulcus of the test subject is wrongly mapped to the postcentral sulcus of the template, so that BA2 is misregistered, as shown by the green outline in Fig(a). During task-optimal training, our method interrupts the geometry of the postcentral sulcus in the template because the uninterrupted postcentral sulcus in the template is inconsistent with localizing BA2 in the training subjects. The final template is shown in Fig(c). We see that the BA2 of the subject (green) and the task-optimal template (black) are well-aligned, although there still exists localization error in the superior end of BA2. | ||
| + | |||
| + | <gallery> | ||
| + | Image:BA2_template.png|Initial Template | ||
| + | Image:BA2_subject.png|Test Subject | ||
| + | Image:BA2_final_template.png|Final Template | ||
| + | </gallery> | ||
| − | + | The video below visualizes the template at each iteration of the optimization. | |
| − | + | <gallery>Image:lh.pm14686.BA2.gif</gallery> | |
| − | + | == (2) Localizing fMRI-defined MT+ Using Cortical Folding == | |
| − | + | In this experiment, we consider 42 subjects with fMRI-defined MT+. MT+ is thought to include the cytoarchitectonically-defined MT, as well as, a small part of the medial superior temporal region. We use the ex-vivo MT template to predict MT+ in the 42 in-vivo subjects. We see that once again, task-optimal template achieves better localization results than FreeSurfer. | |
| − | + | <gallery>Image:exvivoMTPredictsInvivoMT.png</gallery> | |
| − | + | == (2b) Cross-validating In-vivo Subjects == | |
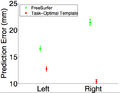
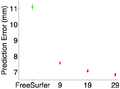
| + | We now perform cross-validation within the in-vivo data set. We consider 9, 19 or 29 training subjects for the task-optimal template. For FreeSurfer, there is no training, so there is only 1 data point. Like before, task-optimal template achieves lower localization errors. | ||
| + | <gallery> | ||
| + | Image:To.LeftInvivoCrossValidation.png|Initial Template | ||
| + | Image:To.RightInvivoCrossValidation.png|Test Subject | ||
| + | </gallery> | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
= Key Investigators = | = Key Investigators = | ||
| − | * MIT: | + | * MIT: [http://people.csail.mit.edu/ythomas/ B.T. Thomas Yeo], Mert Sabuncu, Polina Golland |
| + | * MGH: Bruce Fischl, Daphne Holt | ||
| + | * INRIA: Tom Vercauteren | ||
| + | * Aachen University: Katrin Amunts | ||
| + | * Research Center Juelich: Karl Zilles | ||
= Publications = | = Publications = | ||
| − | |||
| − | |||
| − | |||
| + | [http://www.na-mic.org/publications/pages/display?search=Task-optimal NA-MIC Publications Database on Learning Task-Optimal Registration Cost Functions] | ||
[[Category: Registration]] [[Category:Segmentation]] | [[Category: Registration]] [[Category:Segmentation]] | ||
Latest revision as of 03:14, 6 November 2010
Home < Projects:LearningRegistrationCostFunctionsBack to NA-MIC Collaborations, MIT Algorithms, MGH Algorithms
Learning Task-Optimal Registration Cost Functions
We present a framework for learning the parameters of registration cost functions. The parameters of the registration cost function -- for example, the tradeoff between the image similarity and regularization terms -- are typically determined manually through inspection of the image alignment and then fixed for all applications. We propose a principled approach to learn these parameters with respect to particular applications.
Image registration is ambiguous. For example, the figures below show two subjects with Brodmann areas overlaid on their cortical folding patterns. Brodmann areas are parcellation of the cortex based on the cellular architecture of the cortex. Here, we see that perfectly aligning the inferior frontal sulcus will misalign the superior end of BA44 (Broca's language area). If our goal is segment sulci and gyri, perfectly alignment of the cortical folding pattern is ideal. But it is unclear whether perfectly aligning cortical folds is optimal for localizing Brodmann areas. Here, we show that by taking into account the end-goal of registration, we not only improve the application performance but also potentially eliminate ambiguities in image registration.
Description
The key idea is to introduce a second layer of optimization over and above the usual registration. This second layer of optimization traverses the space of local minima, selecting registration parameters that result in good registration local minima as measured by the performance of the specific application in a training data set. The training data provides additional information not present in a test image, allowing the task-specific cost function to be evaluated during training. For example, if the task is segmentation, we assume the existence of a training data set with ground truth segmentation and a smooth cost function that evaluates segmentation accuracy. This segmentation accuracy is used as a proxy to evaluate registration accuracy.
If the registration cost function employs a single parameter, then the optimal parameter value can be found by exhaustive search. With multiple parameters, exhaustive search is not possible. Here, we demonstrate the optimization of thousands of parameters by gradient descent on the space of local minima, selecting registration parameters that result in good registration local minima as measured by the task-specific cost function in the training data set.
Our formulation is related to the use of continuation methods in computing the entire path of solutions of learning problems (e.g., SVM or Lasso) as a function of a single regularization parameter. Because we deal with multiple (thousands of) parameters, it is impossible for us to compute a solution manifold. Instead, we trace a path within the solution manifold that improves the task-specific cost function.
Another advantage of our approach is that we do not require ground truth deformations. As suggested in the example above, the concept of “ground truth deformations” may not always be well-defined, since the optimal registration may depend on the application at hand. In contrast, our approach avoids the need for ground truth deformations by focusing on the application performance, where ground truth (e.g., via segmentation labels) is better defined.
Experimental Results
We instantiate the framework for the alignment of hidden labels whose extents are not necessarily well-predicted by local image features. We consider the generic weighted Sum of Squared Differences (wSSD) cost function and estimate either (1) the optimal weights or (2) cortical folding template for localizing cytoarchitectural and functional regions based only on macroanatomical cortical folding information. We demonstrate state-of-the-art localization results in both histological and fMRI data sets.
(1) Localizing Brodmann Areas Using Cortical Folding
In this experiment, we estimate the optimal template in the wSSD cost function for localizing Brodmann areas in 10 histologically-analyzed subjects. We compare 3 algorithms: task-optimal template (red), FreeSurfer (green) [1] and optimal uniform weights of the wSSD (black). The optimal uniform weights of the wSSD are found by setting all the weights to a single value and performing an exhaustive search of the weights. We see in the figure below, that task-optimal framework achieves the lowest localization errors.
(1b) Interpreting Task-Optimal Template Estimation
Fig(a) shows the initial cortical geometry of a template subject with its corresponding BA2 in black outline. In this particular subject, the postcentral sulcus is more prominent than the central sulcus. Fig(b) shows the cortical geometry of a test subject together with its BA2. In this subject, the central sulcus is more prominent than the postcentral sulcus. Consequently, in the uniform-weights method, the central sulcus of the test subject is wrongly mapped to the postcentral sulcus of the template, so that BA2 is misregistered, as shown by the green outline in Fig(a). During task-optimal training, our method interrupts the geometry of the postcentral sulcus in the template because the uninterrupted postcentral sulcus in the template is inconsistent with localizing BA2 in the training subjects. The final template is shown in Fig(c). We see that the BA2 of the subject (green) and the task-optimal template (black) are well-aligned, although there still exists localization error in the superior end of BA2.
The video below visualizes the template at each iteration of the optimization.
(2) Localizing fMRI-defined MT+ Using Cortical Folding
In this experiment, we consider 42 subjects with fMRI-defined MT+. MT+ is thought to include the cytoarchitectonically-defined MT, as well as, a small part of the medial superior temporal region. We use the ex-vivo MT template to predict MT+ in the 42 in-vivo subjects. We see that once again, task-optimal template achieves better localization results than FreeSurfer.
(2b) Cross-validating In-vivo Subjects
We now perform cross-validation within the in-vivo data set. We consider 9, 19 or 29 training subjects for the task-optimal template. For FreeSurfer, there is no training, so there is only 1 data point. Like before, task-optimal template achieves lower localization errors.
Key Investigators
- MIT: B.T. Thomas Yeo, Mert Sabuncu, Polina Golland
- MGH: Bruce Fischl, Daphne Holt
- INRIA: Tom Vercauteren
- Aachen University: Katrin Amunts
- Research Center Juelich: Karl Zilles
Publications
NA-MIC Publications Database on Learning Task-Optimal Registration Cost Functions