Projects:NerveSegmentation

Back to NA-MIC Collaborations, MIT Algorithms,

Nerve Segmentation

Automatic segmentation of neural tracts in the dural sac and outside of the spinal canal is important for diagnosis and surgical planning. The variability in intensity, contrast, shape and direction of nerves in high resolution MR images makes segmentation a challenging task.

In this project, we present an automatic tracking method for nerve segmentation based on particle filters. We develop a novel approach to particle representation and dynamics, based on Bezier splines. Moreover, we introduce a robust image likelihood model that enables delineation of nerve bundles and ganglia from the surrounding anatomical structures. In the results section below, we summarize accurate and fast nerve tracking when compared to expert manual segmentation.

Data

We show three slices of an example High-Resolution MR scan. All arrows point to the same nerve bundle. Blue arrows show examples of poor contrast between the nerve and the surrounding tissue; orange arrows indicate the thickening of the neural tract into a ganglion.

Description

We present a tracking approach based on particle filtering, also known as sequential Monte Carlo tracking. Tracking has also been used successfully for segmentation of tubular structures. Most vessel tracking methods model the state as a cross-sectional ellipse or as a cylindroid. In tracking nerve bundles, the regions of low contrast require the state to capture substantially longer segments of the track than what is represented by a cross-section. In addition, nerves tend to change direction, often sharply, which necessitates a use of more complex descriptors than cylinders. Several of the data features can be seen in the Data section above.

To address the challenges of nerve tracking, we define a flexible particle representation that captures the geometric behavior of the nerve bundles. We use a Bezier spline centerline with a linear radius function to characterize a nerve bundle. We devise a dynamics model for particle updates that encourages continuity and smoothness. Furthermore, we define an image likelihood model that compares gradient fields and intensities of predicted patches with image observations to evaluate a posterior distribution of the particles' importance. With the particle model, dynamics model and likelihood model, we can implement a full particle filter. Once tracking is completed, we remove spurious segmentations by measuring the quality of the entire tract.

To the best of our knowledge, this method is the first automatic segmentation of nerve bundles and ganglia.

Results

Left: Example segmentation results – the rightmost nerve shows results without post-processing pruning, while the left segmentation was processed after completion of tracking. as described at the end of Section 2. Right: Cumulative distribution functions of distances (in voxels) between the automatically extracted and manual segmentations: centerline distances on top and surfaces on the bottom. Blue plots indicate differences from algorithm to expert segmentation voxels, red plots correspond to expert-to-algorithm distances. Error bars indicate standard deviations. Dotted vertical lines indicate mean (lower) and 90th percentiles distances (higher).

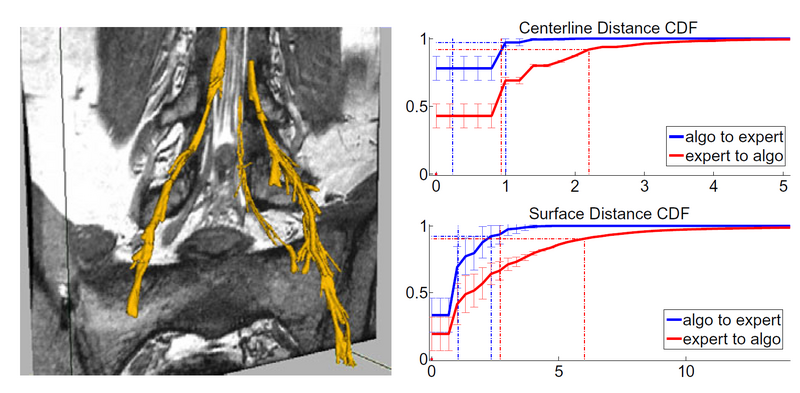
We demonstrate our method on MRI scans of the spine in ten nerve bundles from five subjects. We obtain both expert and automatic segmentations of nerve bundles and ganglia that were deemed traceable, and evaluate tracing accuracy for all bundles.

The mean distance between automatically extracted centerlines and their manual counterparts is within 1 voxel, 90% of automatically extracted centerlines are within 0.9 voxels of the expert centerline, and 90% of expert centerlines are within 2.2 voxels of the algorithm centerline. Visually, we find very good centerline alignment (≤ 1 voxel) inside the vertebral canal. The greater disagreement is present in the ganglia, where the algorithm tends to under-segment and may be off-center, thereby shifting the centerline by a couple of voxels.

We find that since the edges of nerve bundles and ganglia are subject to the partial volume effects and are often near other anatomical structures, the algorithm slightly over-estimates the extent of the nerves in some regions of the image. As mentioned above, inside the thick ganglia the algorithm under-segments due to the ganglia’s more irregular shape. The mean distance from the automatically extracted surface to the expert surface is 1.1 voxels and the 90th percentile is at 2.3 voxels. Visual inspection reveals that the expert segmentation can be irregular and include small deformations or protrusions, especially in pathologies. Since the algorithm attempts to maintain the estimation within the ganglia, the correct outer surface voxels in areas of small irregularities will be more distant from the algorithm prediction. This occurs in cases where the nerve bundle is thicker, generally leading up to and including the ganglia, which can reach 15 voxels in diameter. This results in a mean distance between surfaces of 2.6 with the 90th percentile within 5.9. We therefore conclude that the proposed segmentation may slightly over-segment (usually by no more than two voxels) in thin areas and under-segment in thick areas, but will give a very good estimation of the nerve core and location.

We also evaluated the algorithm on the nerves following the ganglia, where they split up into several thinner peripheral nerves. Here, the algorithm often loses some nerves due to loss of contrast and the small radii of the nerves. When the algorithm continues to track, we observe a fully estimated path (the segmentation follows the nerve), but with over-segmentation as the filter is driven by stronger edges from the neighboring anatomical structures.

Conclusion

As shown in the results, the proposed segmentation may slightly over-segment (usually by at most two voxels) in thin areas and under-segment in thick areas, but will give a very good estimation of the nerve core and location.

Key Investigators

• MIT: Adrian Dalca, Polina Golland
• BWH: Giovanna Danagoulian, Ehud Schmidt, Ron Kikinis