Difference between revisions of "Projects:NerveSegmentation"
| (21 intermediate revisions by 3 users not shown) | |||
| Line 3: | Line 3: | ||
= Nerve Segmentation = | = Nerve Segmentation = | ||
| − | Automatic segmentation of neural tracts in the dural sac and outside of the spinal canal is important for diagnosis and surgical planning. The variability in intensity, contrast, shape and direction of nerves in high resolution MR images makes segmentation a challenging task | + | Automatic segmentation of neural tracts in the dural sac and outside of the spinal canal is important for diagnosis and surgical planning. The variability in intensity, contrast, shape and direction of nerves in high resolution MR images makes segmentation a challenging task. |
| + | In this project, we present an automatic tracking method for nerve segmentation based on particle filters. We develop a novel approach to particle representation and dynamics, based on Bezier splines. Moreover, we introduce a robust image likelihood model that enables delineation of nerve bundles and ganglia from the surrounding anatomical structures. In the results section below, we summarize accurate and fast nerve tracking when compared to expert manual segmentation. | ||
= Data = | = Data = | ||
| − | [[File: | + | [[File:NerveSegMRE2.png|800px|thumb|center|We show four slices of an example High-Resolution MR scan. The blue outline in the first figure shows a manual segmentation of a nerve for reference. All arrows point to the same nerve bundle. Blue arrows show examples of poor contrast between the nerve and the surrounding tissue; orange arrows indicate the thickening of the neural tract into a ganglion. |
]] | ]] | ||
= Description = | = Description = | ||
| − | + | We present a tracking approach based on particle filtering, also known as sequential Monte Carlo tracking. Tracking has also been used successfully for segmentation of tubular structures. Most vessel tracking methods model the state as a cross-sectional ellipse or as a cylindroid. In tracking nerve bundles, the regions of low contrast require the state to capture substantially longer segments of the track than what is represented by a cross-section. In addition, nerves tend to change direction, often sharply, which necessitates a use of more complex descriptors than cylinders. Several of the data features can be seen in the Data section above. | |
| − | To address the challenges of nerve tracking, we define a flexible particle representation that captures the geometric behavior of the nerve bundles. We use a Bezier spline centerline with a linear radius function to characterize a nerve bundle. We devise a dynamics model for particle updates that encourages continuity and smoothness. Furthermore, we define an image likelihood model that compares gradient fields and intensities of predicted patches with image observations to evaluate a posterior distribution of the particles' importance. Once tracking is completed, we remove spurious segmentations by measuring the quality of the entire tract. | + | To address the challenges of nerve tracking, we define a flexible particle representation that captures the geometric behavior of the nerve bundles. We use a Bezier spline centerline with a linear radius function to characterize a nerve bundle. We devise a dynamics model for particle updates that encourages continuity and smoothness. Furthermore, we define an image likelihood model that compares gradient fields and intensities of predicted patches with image observations to evaluate a posterior distribution of the particles' importance. With the particle model, dynamics model and likelihood model, we can implement a full particle filter. Once tracking is completed, we remove spurious segmentations by measuring the quality of the entire tract. |
| + | |||
| + | To the best of our knowledge, this method is the first automatic segmentation of nerve bundles and ganglia. | ||
= Results = | = Results = | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | [[File:NerveSegResultsGraphs.png|800px|thumb|center| | |
| + | Left: Summary of synthetic results for the eight types of synthetic nerves and backgrounds. The | ||
| + | red bars indicate the average of the median distance between the automatic and the manual outline. The | ||
| + | blue bars indicate the 90th percentile. For each category, Model indicates that we generated the nerve | ||
| + | via our particle model, and Expert indicates nerves generated from the smoothed expert segmentation | ||
| + | of real nerves. Right: Summary of the 12 segmentation results on real patient data. The red bars indicate the | ||
| + | medians of distance between the automatic and the expert segmentation; the blue bars indicate the | ||
| + | 90th percentile, in voxels.]] | ||
| + | |||
| + | [[File:NerveSegResults3D.png|800px|thumb|center| | ||
| + | Patient data results. Left: Rendered segmentation results a herniated disk (manually | ||
| + | segmented, yellow) is impinging on the nerve tracts (segmented with our algorithm with minimal user | ||
| + | input, green). Right: Slice that includes a section of a nerve and a ganglion. The yellow outline | ||
| + | indicates the automatic delineation of the nerve. The algorithm tends to slightly under-segment the | ||
| + | nerve, as we see the margins of the nerve underneath the segmentation.]] | ||
| + | |||
| + | We evaluate our algorithm on synthetic and patient data. We show that it can | ||
| + | fully segment the nerves from the initial input point up to the end of the ganglia, | ||
| + | and provide accurate estimates of the nerve thickness. To quantify the accuracy of our | ||
| + | method, we measure the distances between the desired and automatic nerve surfaces. | ||
| + | |||
| + | First, we generate synthetic nerve tracks via our particle model. We vary the dynamics | ||
| + | parameters, such as the radius and control points, beyond ranges that are observed in | ||
| + | real images, to allow for tracks with more irregular behavior. The image intensity is | ||
| + | then formed by adding white noise to the predicted nerve image. We superimpose the nerve | ||
| + | tracks on backgrounds with no noise (blank), Gaussian noise, Perlin noise, and random sections of MRI volumes, which present varying | ||
| + | degrees of segmentation dificulty. | ||
| + | |||
| + | We evaluate the algorithm on 20 images with each background. Typical diameters measure between | ||
| + | four and ten voxels, yielding many partial volume voxels between nerve and background. | ||
| + | We also construct and test a second synthetic dataset of the same size, where the | ||
| + | initial nerve intensity is generated from smoothed binary map of expert nerve | ||
| + | segmentation in patient data. The nerve and background noise models are applied in | ||
| + | the same manner as in the first synthetic set. The nerves range from four to 25 voxels | ||
| + | in diameter, and present with far more irregular shape. | ||
| + | The median distance between the automatically extracted and true nerve surfaces for each nerve generated from our particle model is | ||
| + | 0.8±0.4 voxels, with a 90th percentile of 2.1±0.7 voxels. Most of the algorithm errors are in the edge, partial-volume voxels. For nerves generated from expert segmentations, | ||
| + | the shape irregularity results in an increased median distance between the automatically extracted and true nerve surfaces of 1.3 ± 0.3 voxels, with the 90th percentile of | ||
| + | 4.1 ± 0.4 voxels. | ||
| + | |||
| − | |||
| − | + | We further demonstrate our method on MRI spine scans of 12 nerve bundle segmen- | |
| + | tations from six subjects. The scans were acquired 3D Wide-band Steady State Free | ||
| + | Precession sequence. These | ||
| + | include four nerves in two pathologies where the nerves have been displaced by disk | ||
| + | herniations. We obtain both expert and automatic segmentations of nerve bundles inside | ||
| + | the spine and ganglia that were deemed traceable, and evaluate tracing accuracy | ||
| + | for all bundles. Figure 3 illustrates an example automatic segmentation. | ||
| + | Quantitative results are summarized in Figure 2. The nerve diameters range from | ||
| + | three to six voxels inside the spine and up to about 25 voxels in the ganglia. We find | ||
| + | that the median distance between the automatically extracted and the expert surface | ||
| + | is 1.0 voxel for most nerves, and the 90th percentile is 2.9 ± 0.6 voxels. | ||
| + | = Conclusion = | ||
| + | As shown in the results, the proposed segmentation may slightly over-segment (usually by at most two voxels) in thin areas and under-segment in thick areas, but will give a very good estimation of the nerve core and location. | ||
| − | + | =Key Investigators= | |
* MIT: Adrian Dalca, Polina Golland | * MIT: Adrian Dalca, Polina Golland | ||
| − | * BWH: Giovanna Danagoulian, Ehud Schmidt | + | * BWH: Giovanna Danagoulian, Ehud Schmidt, Ron Kikinis |
| + | |||
| + | = Publications = | ||
| + | *[http://www.na-mic.org/publications/pages/display?search=Projects%3ANerveSegmentation&submit=Search&words=all&title=checked&keywords=checked&authors=checked&abstract=checked&sponsors=checked&searchbytag=checked| NA-MIC Publications Database on nerve segmentation] | ||
Latest revision as of 19:44, 28 November 2012
Home < Projects:NerveSegmentationBack to NA-MIC Collaborations, MIT Algorithms,
Nerve Segmentation
Automatic segmentation of neural tracts in the dural sac and outside of the spinal canal is important for diagnosis and surgical planning. The variability in intensity, contrast, shape and direction of nerves in high resolution MR images makes segmentation a challenging task.
In this project, we present an automatic tracking method for nerve segmentation based on particle filters. We develop a novel approach to particle representation and dynamics, based on Bezier splines. Moreover, we introduce a robust image likelihood model that enables delineation of nerve bundles and ganglia from the surrounding anatomical structures. In the results section below, we summarize accurate and fast nerve tracking when compared to expert manual segmentation.
Data
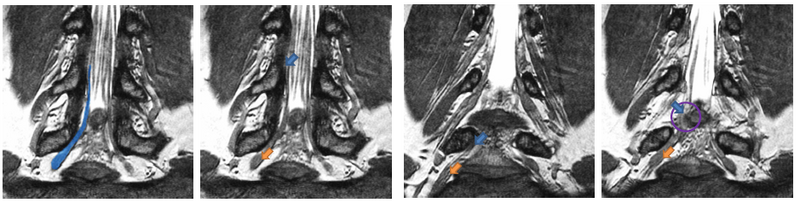
Description
We present a tracking approach based on particle filtering, also known as sequential Monte Carlo tracking. Tracking has also been used successfully for segmentation of tubular structures. Most vessel tracking methods model the state as a cross-sectional ellipse or as a cylindroid. In tracking nerve bundles, the regions of low contrast require the state to capture substantially longer segments of the track than what is represented by a cross-section. In addition, nerves tend to change direction, often sharply, which necessitates a use of more complex descriptors than cylinders. Several of the data features can be seen in the Data section above.
To address the challenges of nerve tracking, we define a flexible particle representation that captures the geometric behavior of the nerve bundles. We use a Bezier spline centerline with a linear radius function to characterize a nerve bundle. We devise a dynamics model for particle updates that encourages continuity and smoothness. Furthermore, we define an image likelihood model that compares gradient fields and intensities of predicted patches with image observations to evaluate a posterior distribution of the particles' importance. With the particle model, dynamics model and likelihood model, we can implement a full particle filter. Once tracking is completed, we remove spurious segmentations by measuring the quality of the entire tract.
To the best of our knowledge, this method is the first automatic segmentation of nerve bundles and ganglia.
Results


We evaluate our algorithm on synthetic and patient data. We show that it can fully segment the nerves from the initial input point up to the end of the ganglia, and provide accurate estimates of the nerve thickness. To quantify the accuracy of our method, we measure the distances between the desired and automatic nerve surfaces.
First, we generate synthetic nerve tracks via our particle model. We vary the dynamics parameters, such as the radius and control points, beyond ranges that are observed in real images, to allow for tracks with more irregular behavior. The image intensity is then formed by adding white noise to the predicted nerve image. We superimpose the nerve tracks on backgrounds with no noise (blank), Gaussian noise, Perlin noise, and random sections of MRI volumes, which present varying degrees of segmentation dificulty.
We evaluate the algorithm on 20 images with each background. Typical diameters measure between four and ten voxels, yielding many partial volume voxels between nerve and background. We also construct and test a second synthetic dataset of the same size, where the initial nerve intensity is generated from smoothed binary map of expert nerve segmentation in patient data. The nerve and background noise models are applied in the same manner as in the first synthetic set. The nerves range from four to 25 voxels in diameter, and present with far more irregular shape. The median distance between the automatically extracted and true nerve surfaces for each nerve generated from our particle model is 0.8±0.4 voxels, with a 90th percentile of 2.1±0.7 voxels. Most of the algorithm errors are in the edge, partial-volume voxels. For nerves generated from expert segmentations, the shape irregularity results in an increased median distance between the automatically extracted and true nerve surfaces of 1.3 ± 0.3 voxels, with the 90th percentile of 4.1 ± 0.4 voxels.
We further demonstrate our method on MRI spine scans of 12 nerve bundle segmen- tations from six subjects. The scans were acquired 3D Wide-band Steady State Free Precession sequence. These include four nerves in two pathologies where the nerves have been displaced by disk herniations. We obtain both expert and automatic segmentations of nerve bundles inside the spine and ganglia that were deemed traceable, and evaluate tracing accuracy for all bundles. Figure 3 illustrates an example automatic segmentation. Quantitative results are summarized in Figure 2. The nerve diameters range from three to six voxels inside the spine and up to about 25 voxels in the ganglia. We find that the median distance between the automatically extracted and the expert surface is 1.0 voxel for most nerves, and the 90th percentile is 2.9 ± 0.6 voxels.
Conclusion
As shown in the results, the proposed segmentation may slightly over-segment (usually by at most two voxels) in thin areas and under-segment in thick areas, but will give a very good estimation of the nerve core and location.
Key Investigators
- MIT: Adrian Dalca, Polina Golland
- BWH: Giovanna Danagoulian, Ehud Schmidt, Ron Kikinis