Difference between revisions of "Projects:AutomatedShapeModelConstruction"
| Line 3: | Line 3: | ||
'''Objective:''' We are developing a new method for automatically constructing shape models, including defining boundary correspondences on shapes in a population. This method can be directly applied to segmentations of brain structures from structural MRI. | '''Objective:''' We are developing a new method for automatically constructing shape models, including defining boundary correspondences on shapes in a population. This method can be directly applied to segmentations of brain structures from structural MRI. | ||
| − | '''Progress:''' We have implemented a software tool to automatically construct shape models from an input of several binary segmentations. This method finds boundary correspondences by creating the most efficient probability distribution for the population of input shapes. The shape models output by our method can then be used to compare differences in brain structure shape between healthy controls and | + | '''Progress:''' We have implemented a software tool to automatically construct shape models from an input of several binary segmentations. This method finds boundary correspondences by creating the most efficient probability distribution for the population of input shapes. The shape models output by our method can then be used to compare differences in brain structure shape between healthy controls and patients with neuropsychiatric disorders. We are investigating the power of this method in statistical group comparisons. |
| + | |||
| + | This method is currently being applied to studying shape changes in the hippocampus and caudate between normal and schizophrenic groups in collaboration with Harvard. We have also extended the method from single figure anatomical objects to a formulation of the multi-object correspondence optimization, and have applied it to a proof-of-concept application to the analysis of brain structure complexes from a longitudinal study of pediatric autism that is underway at UNC Chapel Hill. | ||
| + | |||
| + | ''References:'' | ||
| + | * J. Cates, P.T. Fletcher, M. Styner, M. Shenton, R. Whitaker. Shape Modeling and Analysis with Entropy-Based Particle Systems. IPMI 2007, accepted. | ||
| + | * J. Cates, P.T. Fletcher, R. Whitaker. Entropy-Based Particle Systems for Shape Corresopndence. Mathematical Foundations of Computational Anatomy Workshop, MICCAI 2006. pp. 90-99 Oct 2006. | ||
'''Key Investigators:''' | '''Key Investigators:''' | ||
| Line 9: | Line 15: | ||
* Utah: Joshua Cates, Miriah Meyer, Tom Fletcher, Ross Whitaker | * Utah: Joshua Cates, Miriah Meyer, Tom Fletcher, Ross Whitaker | ||
* Harvard PNL: Sylvain Bouix, Marc Niethammer, Doug Markant, Adam Cohen, Mark Dreusicke, Jim Levitt, Martha Shenton | * Harvard PNL: Sylvain Bouix, Marc Niethammer, Doug Markant, Adam Cohen, Mark Dreusicke, Jim Levitt, Martha Shenton | ||
| + | * UNC: Martin Styner, Heather Cody Hazlett, Joe Piven | ||
| + | |||
| + | '''Links:''' | ||
| + | |||
| + | [[Algorithm:Utah|Utah Algorithms Page]] | ||
| + | |||
| + | {| | ||
| + | |[[Image:Lcomb-grayscale.png|thumbnail|Figure 1]] | ||
| + | |[[Image:Rcomb-grayscale.png|thumbnail|Figure 2]] | ||
| + | |[[Image:meanviews.png|thumbnail|Figure 3]] | ||
| + | |} | ||
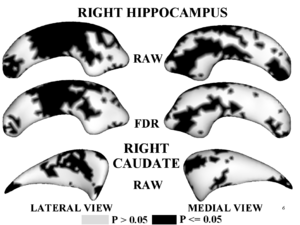
| + | Figure 1,2 illustrates results of hypothesis testing for group differences from the control population for the left/right hippocampus and the left/right caudate. Raw and FDR-corrected p-values are given. Areas of significant group differences ($p <= 0.05$) are shown as dark regions. Areas with insignificant group differences ($p > 0.05$) are shown as light regions. Our results correlate with with other published hypothesis testing results on this data. | ||
| + | |||
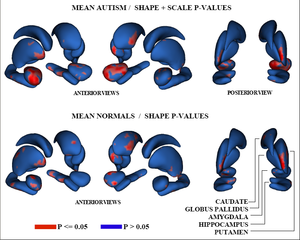
| + | Figure 3 shows the raw p-values from hypothesis testing for group differences as color-maps on mean shapes of the autism group (top row) and the normal control group (bottom row). | ||
Revision as of 21:51, 19 April 2007
Home < Projects:AutomatedShapeModelConstructionBack to NA-MIC_Collaborations
Objective: We are developing a new method for automatically constructing shape models, including defining boundary correspondences on shapes in a population. This method can be directly applied to segmentations of brain structures from structural MRI.
Progress: We have implemented a software tool to automatically construct shape models from an input of several binary segmentations. This method finds boundary correspondences by creating the most efficient probability distribution for the population of input shapes. The shape models output by our method can then be used to compare differences in brain structure shape between healthy controls and patients with neuropsychiatric disorders. We are investigating the power of this method in statistical group comparisons.
This method is currently being applied to studying shape changes in the hippocampus and caudate between normal and schizophrenic groups in collaboration with Harvard. We have also extended the method from single figure anatomical objects to a formulation of the multi-object correspondence optimization, and have applied it to a proof-of-concept application to the analysis of brain structure complexes from a longitudinal study of pediatric autism that is underway at UNC Chapel Hill.
References:
- J. Cates, P.T. Fletcher, M. Styner, M. Shenton, R. Whitaker. Shape Modeling and Analysis with Entropy-Based Particle Systems. IPMI 2007, accepted.
- J. Cates, P.T. Fletcher, R. Whitaker. Entropy-Based Particle Systems for Shape Corresopndence. Mathematical Foundations of Computational Anatomy Workshop, MICCAI 2006. pp. 90-99 Oct 2006.
Key Investigators:
- Utah: Joshua Cates, Miriah Meyer, Tom Fletcher, Ross Whitaker
- Harvard PNL: Sylvain Bouix, Marc Niethammer, Doug Markant, Adam Cohen, Mark Dreusicke, Jim Levitt, Martha Shenton
- UNC: Martin Styner, Heather Cody Hazlett, Joe Piven
Links:
Figure 1,2 illustrates results of hypothesis testing for group differences from the control population for the left/right hippocampus and the left/right caudate. Raw and FDR-corrected p-values are given. Areas of significant group differences ($p <= 0.05$) are shown as dark regions. Areas with insignificant group differences ($p > 0.05$) are shown as light regions. Our results correlate with with other published hypothesis testing results on this data.
Figure 3 shows the raw p-values from hypothesis testing for group differences as color-maps on mean shapes of the autism group (top row) and the normal control group (bottom row).