Difference between revisions of "Projects:KPCA LLE KLLE ShapeAnalysis"
| (11 intermediate revisions by 3 users not shown) | |||
| Line 1: | Line 1: | ||
| − | Back to | + | Back to [[Algorithm:Stony Brook|Stony Brook University Algorithms]] |
| − | + | __NOTOC__ | |
= KPCA LLE KLLE Shape Analysis = | = KPCA LLE KLLE Shape Analysis = | ||
| Line 13: | Line 13: | ||
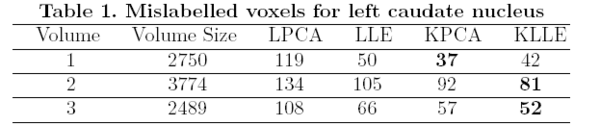
[[Image:Table1.png|thumb|600px|Figure 1: Table gives the number of mislabelled voxels for each of the methods for left caudate nucleus]] | [[Image:Table1.png|thumb|600px|Figure 1: Table gives the number of mislabelled voxels for each of the methods for left caudate nucleus]] | ||
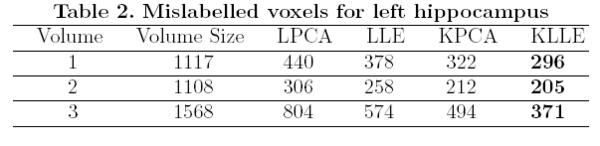
| − | [[Image:Table2.png|thumb|600px|Figure 2 | + | [[Image:Table2.png|thumb|600px|Figure 2: Table gives the number of mislabelled voxels for each of the methods for left hippocampus]] |
= Key Investigators = | = Key Investigators = | ||
| − | * Georgia Tech: Yogesh Rathi, Samuel Dambreville, Allen Tannenbaum | + | * Georgia Tech Algorithms: Yogesh Rathi, Samuel Dambreville, Allen Tannenbaum |
= Publications = | = Publications = | ||
''In Print'' | ''In Print'' | ||
| − | * [http://www.na-mic.org/ | + | * [http://www.na-mic.org/publications/pages/display?search=KPCA+LLE+KLLE+ShapeAnalysis&submit=Search&words=all&title=checked&keywords=checked&authors=checked&abstract=checked&searchbytag=checked&sponsors=checked| NA-MIC Publications Database on KPCA, LLE, KLLE Shape Analysis] |
| − | |||
| − | |||
| − | + | [[Category: Shape Analysis]] | |
| − | |||
| − | |||
Latest revision as of 00:58, 16 November 2013
Home < Projects:KPCA LLE KLLE ShapeAnalysisBack to Stony Brook University Algorithms
KPCA LLE KLLE Shape Analysis
Our Objective is to compare various shape representation techniques like linear PCA (LPCA), kernel PCA (KPCA), locally linear embedding (LLE) and kernel locally linear embedding (KLLE).
Description
The surfaces are represented as the zero level set of a signed distance function and shape learning is performed on the embeddings of these shapes. We carry out some experiments to see how well each of these methods can represent a shape, given the training set. We tested the performance of these methods on shapes of left caudate nucleus and left hippocampus. The training set of left caudate nucleus consisted of 26 data sets and the test set contained 3 volumes. Error between a particular shape representation and ground truth was calculated by computing the number of mislabeled voxels using each of the methods. Figure 1 gives the error using each of the methods. Similar tests were done on a training set of 20 hippocampus data with 3 test volumes. Figure 2 gives the error table for each of the methods [1].
Key Investigators
- Georgia Tech Algorithms: Yogesh Rathi, Samuel Dambreville, Allen Tannenbaum
Publications
In Print