Difference between revisions of "Projects:PointSetRigidRegistration"
| (24 intermediate revisions by 3 users not shown) | |||
| Line 1: | Line 1: | ||
| − | Back to | + | Back to [[Algorithm:Stony Brook|Stony Brook University Algorithms]] |
__NOTOC__ | __NOTOC__ | ||
| − | = Particle Filtering for Point Set Registration | + | = Particle Filtering with Stochastic Dynamics for Point Set Registration = |
| + | We propose a particle filtering scheme for the registration of 2D and 3D point set undergoing a rigid body transformation. Moreover, we incorporate stochastic dynamics to model the uncertainity of the registration process. | ||
= Description = | = Description = | ||
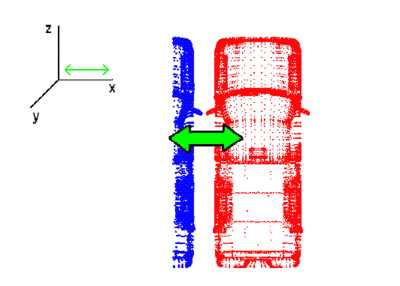
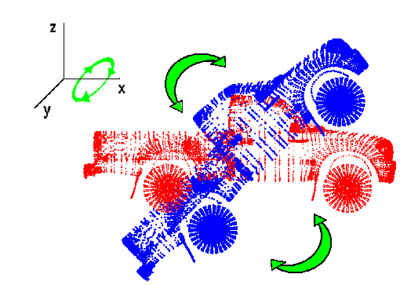
| + | Typically, registration algorithms compute the transformations paramaters by maximizing a metric given an estimate of the correspondence between points across the two sets of interest. This can be viewed as a posterior estimation problem problem, in which the corresponding distribution can naturally be estimated using a particle filter. In this work, we treat motion as a local variation in the pose parameters obatined from running a few iterations of the standard Iterative Closest Point (ICP) algorithm. Employing this idea, we introduce stochastic motion dynamics to widen the narrow band of convergence as well as provide a dynamical model of uncertainity. This is described in the following figure. | ||
| − | + | [[Image:StochasticDynamics_Translation.png|400px]] [[Image:Stochastic.Dynamics_Rotation.png|400px]] | |
| − | + | In the above figure, we demonstrate the notion of uncertainity in point set registration. For this simplistic case, the uncertaintity is given for both pure translation and rotation in the x-axis. | |
| + | |||
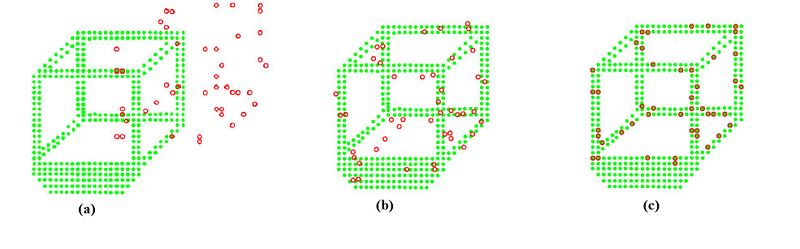
| + | In contrast with other techniques, our approach requires no annealing schedule, which results in a reduction in computational complexity as well as maintains the temoral coherency of the state (no loss of information). Also, unlike most alternative approaches for point set registration, we make no geometric assumptions on the two data sets. One such algorithm is the Kernel Density Correlation (KC) approach. In this algorithm, a global cost function is defined such that the method can be interpreted as a multiply-linked ICP approach. Rather than define a single pair of correspondences, one point set must interact with each point in the opposing set, thereby eliminating point correspondences altogther. Our algorithm can also be re-interpreted as a switch stochastic ICP approach where one point set interacts with only a handful of correspondences. Results are shown below, which deals with the case of differing densities across the two point sets. | ||
| + | |||
| + | [[Image:RegistrationCubeResult PFKCInitial.png|800px]] | ||
| + | |||
| + | In above figure, we generate a new point cloud that has been sampled from the original cube model and then apply a rigid transformation. This is seen in (a). Results obtained from the KC algorithm is seen in (b). Our particle filtering approach successfully found the correct optimal transformation that aligns both point clouds despite the differing geometry around the local neighborhood of a point within their respective sets. | ||
= Key Investigators = | = Key Investigators = | ||
| Line 16: | Line 24: | ||
= Publications = | = Publications = | ||
| − | ''In | + | ''In print'' |
| − | * | + | * [http://www.na-mic.org/publications/pages/display?search=Projects%3APointSetRigidRegistration&submit=Search&words=all&title=checked&keywords=checked&authors=checked&abstract=checked&searchbytag=checked&sponsors=checked| NA-MIC Publications Database on Point Set Rigid Registration on Point Set Rigid Registration] |
[[Category:Registration]] | [[Category:Registration]] | ||
Latest revision as of 00:59, 16 November 2013
Home < Projects:PointSetRigidRegistrationBack to Stony Brook University Algorithms
Particle Filtering with Stochastic Dynamics for Point Set Registration
We propose a particle filtering scheme for the registration of 2D and 3D point set undergoing a rigid body transformation. Moreover, we incorporate stochastic dynamics to model the uncertainity of the registration process.
Description
Typically, registration algorithms compute the transformations paramaters by maximizing a metric given an estimate of the correspondence between points across the two sets of interest. This can be viewed as a posterior estimation problem problem, in which the corresponding distribution can naturally be estimated using a particle filter. In this work, we treat motion as a local variation in the pose parameters obatined from running a few iterations of the standard Iterative Closest Point (ICP) algorithm. Employing this idea, we introduce stochastic motion dynamics to widen the narrow band of convergence as well as provide a dynamical model of uncertainity. This is described in the following figure.
In the above figure, we demonstrate the notion of uncertainity in point set registration. For this simplistic case, the uncertaintity is given for both pure translation and rotation in the x-axis.
In contrast with other techniques, our approach requires no annealing schedule, which results in a reduction in computational complexity as well as maintains the temoral coherency of the state (no loss of information). Also, unlike most alternative approaches for point set registration, we make no geometric assumptions on the two data sets. One such algorithm is the Kernel Density Correlation (KC) approach. In this algorithm, a global cost function is defined such that the method can be interpreted as a multiply-linked ICP approach. Rather than define a single pair of correspondences, one point set must interact with each point in the opposing set, thereby eliminating point correspondences altogther. Our algorithm can also be re-interpreted as a switch stochastic ICP approach where one point set interacts with only a handful of correspondences. Results are shown below, which deals with the case of differing densities across the two point sets.
In above figure, we generate a new point cloud that has been sampled from the original cube model and then apply a rigid transformation. This is seen in (a). Results obtained from the KC algorithm is seen in (b). Our particle filtering approach successfully found the correct optimal transformation that aligns both point clouds despite the differing geometry around the local neighborhood of a point within their respective sets.
Key Investigators
- Georgia Tech: Romeil Sandhu, Samuel Dambreville, Allen Tannenbaum
Publications
In print