Difference between revisions of "Projects:RegistrationRegularization"
| (31 intermediate revisions by 3 users not shown) | |||
| Line 1: | Line 1: | ||
| − | Back to | + | Back to [[Algorithm:MIT|MIT Algorithms]] |
| + | __NOTOC__ | ||
| + | = Registration Regularization = | ||
We propose a unified framework for computing atlases from manually labeled data sets at various degrees of “sharpness” and the joint registration and segmentation of a new brain with these atlases. In non-rigid registration, the tradeoff between warp regularization and image fidelity is typically set empirically. In segmentation, this leads to a probabilistic atlas of arbitrary “sharpness”: weak regularization results in well-aligned training images, producing a “sharp” atlas; strong regularization yields a “blurry” atlas. We study the effects of this tradeoff in the context of cortical surface parcellation, but the framework applies to volume registration as well. This is an important question because of the increasingly availability of atlases in public databases and the development of registration algorithms separate from the atlas construction process. | We propose a unified framework for computing atlases from manually labeled data sets at various degrees of “sharpness” and the joint registration and segmentation of a new brain with these atlases. In non-rigid registration, the tradeoff between warp regularization and image fidelity is typically set empirically. In segmentation, this leads to a probabilistic atlas of arbitrary “sharpness”: weak regularization results in well-aligned training images, producing a “sharp” atlas; strong regularization yields a “blurry” atlas. We study the effects of this tradeoff in the context of cortical surface parcellation, but the framework applies to volume registration as well. This is an important question because of the increasingly availability of atlases in public databases and the development of registration algorithms separate from the atlas construction process. | ||
| Line 14: | Line 16: | ||
<tr> | <tr> | ||
<td> | <td> | ||
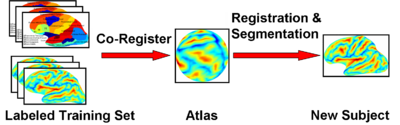
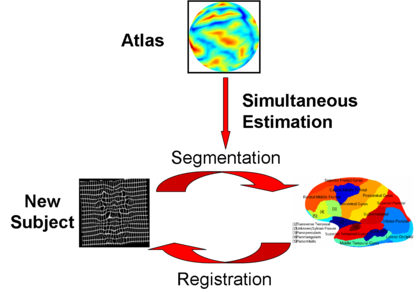
| − | [[Image:JointRegSeg.png|thumb|center| | + | [[Image:JointRegSeg.png|thumb|center|420px| Joint Registration-Segmentation]] |
</td> | </td> | ||
<td> | <td> | ||
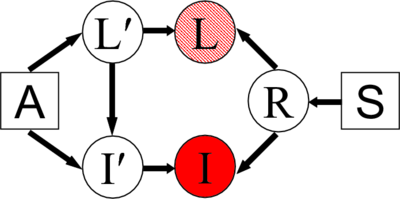
| − | [[Image:GraphicalModel.png|thumb|center| | + | [[Image:GraphicalModel.png|thumb|center|400px|"A" is an atlas used to generate the label map L' in some universal atlas space. The atlas A and label map L' generate image I'. S is the smoothness parameter that generates random warp field R. This warp is then applied to the label map L' and image I' to create the label map L and the image I. We assume the label map L is available for the training images, but not for the test image. The image I is observed in both training and test cases.]] |
</td> | </td> | ||
</tr> | </tr> | ||
| Line 23: | Line 25: | ||
</center> | </center> | ||
| − | We use the generative model to compute atlases from manually labeled data at various degrees of “sharpness” and the joint registration-segmentation of a new brain with these atlases. Using this framework, we investigate the tradeoff between warp regularization and image fidelity, i.e. the smoothness of the new subject warp and the sharpness of the atlas. | + | We use the generative model to compute atlases from manually labeled data at various degrees of “sharpness” and the joint registration-segmentation of a new brain with these atlases. Using this framework, we investigate the tradeoff between warp regularization and image fidelity, i.e. the smoothness of the new subject warp and the sharpness of the atlas. We compare three special cases of our framework, namely: |
| − | |||
| − | We compare three special cases of our framework, namely: | ||
(1) Progressive registration of a new brain to increasingly “sharp” atlases using increasingly flexible warps, by initializing each registration stage with the optimal warps from a “blurrier” atlas. We call this multiple atlases, multiple warp scales (MAMS). | (1) Progressive registration of a new brain to increasingly “sharp” atlases using increasingly flexible warps, by initializing each registration stage with the optimal warps from a “blurrier” atlas. We call this multiple atlases, multiple warp scales (MAMS). | ||
| Line 33: | Line 33: | ||
(3) Registration to a single atlas with fixed constrained warps. We call this single atlas, single warp scale (SASS). | (3) Registration to a single atlas with fixed constrained warps. We call this single atlas, single warp scale (SASS). | ||
| − | We use dice as the measure of segmentation quality. From the graph below, we note that the | + | == Experimental Results == |
| + | |||
| + | We use dice as the measure of segmentation quality. From the graph below, we note that the optimal algorithms correspond to a unique balance between atlas “sharpness” and warp regularization. Our experiments show that the optimal parameter values that correspond to this balance can be determined using cross-validation. The optimal parameter values are robust across subjects, and the same for both co-registration of the training data and registration of a new subject. This suggests that a single atlas at an optimal sharpness is sufficient to achieve the best segmentation results. Furthermore, our experiments also suggest that segmentation accuracy is tolerant up to a small mismatch between atlas sharpness and warp smoothness. | ||
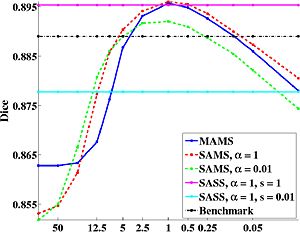
[[Image:AvgResults.jpg|thumb|center|300px|Plot of Dice as a function of the warp smoothness S. Note that S is on a log scale. <math>\alpha</math> corresponds to the sharpness of the atlas used.]] | [[Image:AvgResults.jpg|thumb|center|300px|Plot of Dice as a function of the warp smoothness S. Note that S is on a log scale. <math>\alpha</math> corresponds to the sharpness of the atlas used.]] | ||
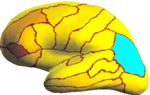
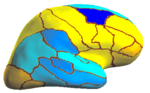
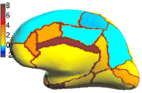
| − | In the figure below, we | + | In the figure below, we display the percentage improvement of SASS over FreeSurfer [1,2]. For each of the 35 structures for each hemisphere, we perform a one-sided paired-sampled t-test between SASS and FreeSurfer, where each subject is considered a sample. We use the False Discovery Rate (FDR) to correct for multiple comparisons. In the left hemisphere, SASS achieves statistically significant improvement over FreeSurfer for 17 structures (FDR < 0.05), while the remaining structures yield no statistical difference. In the right hemisphere, SASS achieves improvement for 11 structures (FDR < 0.05), while the remaining structures yield no statistical difference. The p-values for the left and right hemispheres are pooled together for the False Discovery Rate analysis. |
| + | <center> | ||
| + | <table> | ||
| + | <tr> | ||
| + | <td> | ||
| + | [[Image:Lh.PercentImprove1.png|thumb|center|150px|Left Medial]] | ||
| + | </td> | ||
| + | <td> | ||
| + | [[Image:Lh.PercentImprove2.png|thumb|center|150px|Left Lateral]] | ||
| + | </td> | ||
| + | <td> | ||
| + | [[Image:Rh.PercentImprove2.png|thumb|center|150px|Right Lateral]] | ||
| + | </td> | ||
| + | <td> | ||
| + | [[Image:Rh.PercentImprove1.png|thumb|center|142px|Right Medial]] | ||
| + | </td> | ||
| + | </tr> | ||
| + | </table> | ||
| + | </center> | ||
| Line 47: | Line 67: | ||
= Key Investigators = | = Key Investigators = | ||
| − | * MIT | + | * MIT : [[http://people.csail.mit.edu/ythomas/ | B.T. Thomas Yeo]], Mert Sabuncu, Polina Golland |
| + | * Harvard : Rahul Desikan, Bruce Fischl | ||
= Publications = | = Publications = | ||
| − | |||
| − | |||
| − | + | [http://www.na-mic.org/publications/pages/display?search=Projects:RegistrationRegularization&submit=Search&words=all&title=checked&keywords=checked&authors=checked&abstract=checked&sponsors=checked&searchbytag=checked| NA-MIC Publications Database on Optimal Atlas Regularization in Image Segmentation] | |
| + | |||
| − | |||
[[Category: Registration]] [[Category:Segmentation]] | [[Category: Registration]] [[Category:Segmentation]] | ||
Latest revision as of 20:18, 11 May 2010
Home < Projects:RegistrationRegularizationBack to MIT Algorithms
Registration Regularization
We propose a unified framework for computing atlases from manually labeled data sets at various degrees of “sharpness” and the joint registration and segmentation of a new brain with these atlases. In non-rigid registration, the tradeoff between warp regularization and image fidelity is typically set empirically. In segmentation, this leads to a probabilistic atlas of arbitrary “sharpness”: weak regularization results in well-aligned training images, producing a “sharp” atlas; strong regularization yields a “blurry” atlas. We study the effects of this tradeoff in the context of cortical surface parcellation, but the framework applies to volume registration as well. This is an important question because of the increasingly availability of atlases in public databases and the development of registration algorithms separate from the atlas construction process.
Description
In image registration, one usually optimizes the objective function with two parts. The first term is the similarity between images. The second term regularizes the warp. The smoothness parameter that weights the second term determines the tradeoff between the similarity measure and the regularization. In Atlas-based segmentation, one is given a set of labeled training images. The training images are co-registered to a common space. An atlas that summarizes the information between the image features and the labels is computed in this common space. This atlas is used to segment and normalize a new image.
We employ a generative model for the joint registration and segmentation of images (see figures below). The atlas construction process arises naturally as estimation of the model parameters. This framework allows the computation of unbiased atlases from manually labeled data at various degrees of "sharpness", as well as the joint registration and segmentation of a novel brain in a consistent manner.
We use the generative model to compute atlases from manually labeled data at various degrees of “sharpness” and the joint registration-segmentation of a new brain with these atlases. Using this framework, we investigate the tradeoff between warp regularization and image fidelity, i.e. the smoothness of the new subject warp and the sharpness of the atlas. We compare three special cases of our framework, namely:
(1) Progressive registration of a new brain to increasingly “sharp” atlases using increasingly flexible warps, by initializing each registration stage with the optimal warps from a “blurrier” atlas. We call this multiple atlases, multiple warp scales (MAMS).
(2) Progressive registration to a single atlas with increasingly flexible warps. We call this single atlas, multiple warp scales (SAMS).
(3) Registration to a single atlas with fixed constrained warps. We call this single atlas, single warp scale (SASS).
Experimental Results
We use dice as the measure of segmentation quality. From the graph below, we note that the optimal algorithms correspond to a unique balance between atlas “sharpness” and warp regularization. Our experiments show that the optimal parameter values that correspond to this balance can be determined using cross-validation. The optimal parameter values are robust across subjects, and the same for both co-registration of the training data and registration of a new subject. This suggests that a single atlas at an optimal sharpness is sufficient to achieve the best segmentation results. Furthermore, our experiments also suggest that segmentation accuracy is tolerant up to a small mismatch between atlas sharpness and warp smoothness.
In the figure below, we display the percentage improvement of SASS over FreeSurfer [1,2]. For each of the 35 structures for each hemisphere, we perform a one-sided paired-sampled t-test between SASS and FreeSurfer, where each subject is considered a sample. We use the False Discovery Rate (FDR) to correct for multiple comparisons. In the left hemisphere, SASS achieves statistically significant improvement over FreeSurfer for 17 structures (FDR < 0.05), while the remaining structures yield no statistical difference. In the right hemisphere, SASS achieves improvement for 11 structures (FDR < 0.05), while the remaining structures yield no statistical difference. The p-values for the left and right hemispheres are pooled together for the False Discovery Rate analysis.
[1] Fischl, Sereno and Dale. High-resolution intersubject averaging and a coordinate system for the cortical surface. Human Brain Mapping, 8(4):272--284, 1999
[2] Fischl, van der Kouwe, Destrieux, Halgren, Segonne, Salat, Busa, Seidman, Goldstein, Kennedy, Caviness, Makris, Rosen and Dale. Automatically Parcellating the Human cerebral Cortex. Cerebral Cortex, 14:11--22, 2004
Key Investigators
- MIT : [| B.T. Thomas Yeo], Mert Sabuncu, Polina Golland
- Harvard : Rahul Desikan, Bruce Fischl
Publications
NA-MIC Publications Database on Optimal Atlas Regularization in Image Segmentation