Difference between revisions of "Projects:ProstateRegistration"
| (6 intermediate revisions by the same user not shown) | |||
| Line 1: | Line 1: | ||
| − | Back to [[Algorithm: | + | Back to [[Algorithm:Stony Brook|Stony Brook Algorithms]] |
__NOTOC__ | __NOTOC__ | ||
| − | = | + | = Particle Filter Registration of Medical Imagery = |
| − | + | We transform the general problem of image registration to a sparse task of aligning point clouds. This is accomplished by considering the image as a probability density function, from which a point cloud is formed by randomly drawing samples. This allows us to apply a particle filtering technique for the registration. While point set registration and image registration are generally studied separately, this approach attempts to bridge the two. Thus, our contribution is threefold. Firstly, our method can handle affine transformations. Secondly, registration of partial images is more natural. Lastly, the point cloud representation is much sparser than the usual image representation as a discrete function. This allows us to drastically reduce the computational cost associated with 2D and 3D registration task. | |
| − | = | + | == Prostate registration == |
| − | + | Experimental results demonstrate the fast and robust convergence of the proposed algorithm. See Figures below: | |
| − | |||
| − | |||
One the right side: | One the right side: | ||
| Line 16: | Line 14: | ||
One the left: | One the left: | ||
Blue: The same prostate in prone position; | Blue: The same prostate in prone position; | ||
| − | + | Pink: Result of registering the Yellow (supine) towards the Blue (prone). | |
[[Image:ProstateRegSupineToProneInParaview.png|500px|]] | [[Image:ProstateRegSupineToProneInParaview.png|500px|]] | ||
| + | |||
| + | == DWI registration == | ||
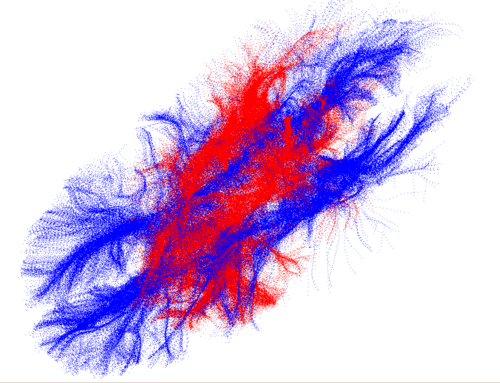
| + | When applying the method to register two point sets generated from DWI images, the local minima of the registration energy is successfully avoided and the figure below shows: | ||
| + | |||
| + | [[Image:BrainBefore.png|500px|]] | ||
| + | |||
| + | Shows the original DWI point set in blue and the affine transformed one in red. The objective is to register the red to the blue. | ||
| + | |||
| + | |||
| + | [[Image:BrainAfter.png|500px|]] | ||
| + | |||
| + | The result of using the particle filter image registration. | ||
= Key Investigators = | = Key Investigators = | ||
Latest revision as of 01:15, 16 November 2013
Home < Projects:ProstateRegistrationBack to Stony Brook Algorithms
Particle Filter Registration of Medical Imagery
We transform the general problem of image registration to a sparse task of aligning point clouds. This is accomplished by considering the image as a probability density function, from which a point cloud is formed by randomly drawing samples. This allows us to apply a particle filtering technique for the registration. While point set registration and image registration are generally studied separately, this approach attempts to bridge the two. Thus, our contribution is threefold. Firstly, our method can handle affine transformations. Secondly, registration of partial images is more natural. Lastly, the point cloud representation is much sparser than the usual image representation as a discrete function. This allows us to drastically reduce the computational cost associated with 2D and 3D registration task.
Prostate registration
Experimental results demonstrate the fast and robust convergence of the proposed algorithm. See Figures below:
One the right side:
Blue: prostate in prone position; Yellow: prostate in supine position.
One the left:
Blue: The same prostate in prone position; Pink: Result of registering the Yellow (supine) towards the Blue (prone).
DWI registration
When applying the method to register two point sets generated from DWI images, the local minima of the registration energy is successfully avoided and the figure below shows:
Shows the original DWI point set in blue and the affine transformed one in red. The objective is to register the red to the blue.
The result of using the particle filter image registration.
Key Investigators
- Georgia Tech Algorithms: Yi Gao, Allen Tannenbaum