Difference between revisions of "Projects:FieldmapFreeDistortionCorrection"
| (50 intermediate revisions by 3 users not shown) | |||
| Line 1: | Line 1: | ||
| − | + | Back to [[NA-MIC_Internal_Collaborations:fMRIAnalysis|NA-MIC Collaborations]], [[Algorithm:MIT|MIT Algorithms]] | |
| − | = | + | __NOTOC__ |
| + | = Fieldmap-Free EPI Distortion Correction = | ||
Echo-planar imaging (EPI) is one of the most widely used pulse sequences in | Echo-planar imaging (EPI) is one of the most widely used pulse sequences in | ||
| Line 21: | Line 22: | ||
however neither fieldmaps, nor knowledge of shim parameters is required. | however neither fieldmaps, nor knowledge of shim parameters is required. | ||
| − | = Registration without Correction = | + | == Registration without Correction == |
Localization of functional information relies on accurate registration of EPI and structural MR, which can be difficult due to EPI distortion caused by B0 field inhomogeneity. Correcting distortion using acquired Fieldmaps has been shown to improve registration [1], but Fieldmaps may not be available or may not be applicable if significant motion is present in the EPI, resulting in sub-optimal registration. | Localization of functional information relies on accurate registration of EPI and structural MR, which can be difficult due to EPI distortion caused by B0 field inhomogeneity. Correcting distortion using acquired Fieldmaps has been shown to improve registration [1], but Fieldmaps may not be available or may not be applicable if significant motion is present in the EPI, resulting in sub-optimal registration. | ||
| Line 29: | Line 30: | ||
|} | |} | ||
| − | = Problem 1: Segmentation = | + | == Problem 1: Segmentation == |
Magnetic field models exist to compute a Fieldmap from a Tissue/Air segmentation [2,3], but segmenting structural MR is difficult due to the similar intensities of bone and air. In the Fieldmap-Free method [4], T1 MRI was segmented using a trained classifier that computes the probability of tissue given MR intensity. | Magnetic field models exist to compute a Fieldmap from a Tissue/Air segmentation [2,3], but segmenting structural MR is difficult due to the similar intensities of bone and air. In the Fieldmap-Free method [4], T1 MRI was segmented using a trained classifier that computes the probability of tissue given MR intensity. | ||
| Line 38: | Line 39: | ||
|} | |} | ||
| − | = Problem 2: Shim Estimation = | + | == Problem 2: Shim Estimation == |
Existing magnetic field models do not account for the shim fields that reduce B0 field inhomogeniety prior to acquisition. Without this information, accurate unwarping is not possible. In this Method, a Fieldmap (without shim) was computed from the Segmented MR using the field model in [2]. | Existing magnetic field models do not account for the shim fields that reduce B0 field inhomogeniety prior to acquisition. Without this information, accurate unwarping is not possible. In this Method, a Fieldmap (without shim) was computed from the Segmented MR using the field model in [2]. | ||
| Line 49: | Line 50: | ||
| − | [1] Cusack et al | + | == Atlas-Based Improved Prediction of Magnetic Field Inhomogeneity for Distortion Correction of EPI Data Motivation == |
| − | [2] Jenkinson et al | + | |
| − | [3] Koch et al | + | In the Fieldmap-Free method described above, it was shown that tissue/air susceptibility models could be derived from structural MRI by using |
| − | [4] Poynton et al | + | an intensity-based classifier trained with CT [4]. It was also shown that registration of the EPI and structural MR could be used to search over the unknown shim |
| + | parameters allowing distortion correction of the EPI that agrees well with results obtained using acquired fieldmaps. | ||
| + | |||
| + | Variability in structural MR acquisitions, however, may limit the efficacy of an intensity-based classifier in cases where the MR | ||
| + | intensity properties differ significantly from those of the training data. In [4], CT data sets with MR acquired on the same scanner as the subjects of interest could be used to train the classifier, but this may not be possible in many cases. Limited anatomical information below the brain may also prevent accurate estimation of the perturbing field. Therefore, obtaining more reliable susceptibility models from structural MR is critical for retrospective unwarping of EPI data sets | ||
| + | that lack acquired fieldmaps. While previous results predicting fieldmaps from structural MR have shown good agreement with acquired | ||
| + | fieldmaps, we hypothesized that improved segmentation methods would result in even greater accuracy. | ||
| + | |||
| + | = Description = | ||
| + | |||
| + | In this work, anatomical information from a set of 22 whole-head CT data sets is used to achieve improved, | ||
| + | subject-specific segmentation of structural MR. A tissue/air atlas is constructed from the CT data to obtain priors on | ||
| + | the probability of tissue or air at each location in the anatomy. The corresponding structural MR is used to train a classifier that | ||
| + | segments the MR of the subject of interest and this is used as input to a first order perturbation field model to compute a | ||
| + | subject-specific fieldmap. The method is evaluated by comparison of predicted fieldmaps and acquired fieldmaps. In addition, | ||
| + | the MR classifier can be used to obtain probabilistic bone segmentations from structural MR that show promising agreement with segmented CT. | ||
| + | |||
| + | == Results == | ||
| + | |||
| + | === Atlas Construction === | ||
| + | |||
| + | We obtained 22 datasets consisting of CT and MRI from 3 sources: the publicly available Retrospective Image Registration | ||
| + | Evaluation (RIRE) database (17 neurosurgery patients), the Radiology department at Brigham and Women's Hospital (BWH) (4 neurosurgery patients) and the Zubal | ||
| + | head phantom (1 subject) [5]. For each subject, the CT data was registered to its corresponding MR. The MR was registered | ||
| + | to standard space and these transformations were then applied to the co-registered CT. Tissue/air labels were obtained by thresholding the CT data in | ||
| + | standard space. Probabilistic tissue/air and air/bone atlases were then constructed [6] and are shown in Fig. 4 below. | ||
| + | |||
| + | {| | ||
| + | |[[Image:Tissue air atlas.jpg|600px|thumb|Fig. 4. Results of Atlas Construction. Tissue / Air (left and center) and Bone atlases (right) constructed from 22 CT data sets.]] | ||
| + | |} | ||
| + | |||
| + | === Atlas-based Segmentation === | ||
| + | |||
| + | Structural MR was segmented using an MR classifier that incorporates spatially | ||
| + | dependent prior information from the probabilistic atlas and MR intensity information (from the subject of interest) to obtain a subject-specific susceptibility | ||
| + | model. The classifier was trained using the CT/MR training data described above, but applied to segment MR data acquired at a separate site. The accuracy of the segmentations was evaluated by comparing fieldmaps predicted | ||
| + | from the atlas-based segmenter to acquired fieldmaps. The fieldmaps were also | ||
| + | compared to those predicted using intensity information alone (ie. a spatially | ||
| + | constant prior). | ||
| + | |||
| + | |||
| + | Results of atlas-based segmentation of structural MR is shown in Fig. 5 below. | ||
| + | T1 of the sinus region is shown on the left. The limitations of using the intensity | ||
| + | classifier to segment the MR is shown in the middle image. While the classifier produces reasonable results for many of the voxels in the sinuses, | ||
| + | voxels outside this region which are clearly soft tissue or | ||
| + | bone are mislabeled with values close to zero. In contrast, using the atlas-based | ||
| + | segmenter (right image) achieves similar results for the highly variable | ||
| + | subject-specific anatomy within the sinus region, while producing fewer errors | ||
| + | in the surrounding area. | ||
| + | |||
| + | |||
| + | Results of the segmentation of bone from structural MR for a representative subject is shown in Fig. 6. The | ||
| + | CT shown on the left can be easily thresholded to segment bone from air and | ||
| + | soft tissue. The results of using the intensity and atlas- | ||
| + | based classifiers are shown in the middle and right images, respectively. While the intensity classifier has some success in | ||
| + | segmenting MR into tissue/air classes, it is much less effective in segmenting | ||
| + | bone. Inspection of the the atlas-based segmentation, however, shows good general agreement with the CT, with a dice score of 0.780 for | ||
| + | this subject. | ||
| + | |||
| + | {| | ||
| + | |[[Image:Tissue air seg.jpg|600px|thumb|Fig. 5. Tissue / Air Segmentation. Tissue probability maps computed from the structural MR show improved segmentation when the tissue/air atlas is incorporated into the MR classifier.]] | ||
| + | |} | ||
| + | |||
| + | |||
| + | |||
| + | {| | ||
| + | |[[Image:Bone air seg.jpg|600px|thumb|Fig. 6. Bone Segmentation. Segmentation of bone from MR using intensity information alone is ineffective (middle), while atlas-based segmentation shows good overall agreement with CT (right).]] | ||
| + | |} | ||
| + | |||
| + | === Fieldmap Estimation === | ||
| + | |||
| + | Fieldmaps are predicted from the atlas and intensity-based segmentations using | ||
| + | the perturbation field model described in [2]. In this model, a first order perturba- | ||
| + | tion solution of Maxwell’s equations is calculated from a tissue/air susceptibility | ||
| + | model, where each pixel takes continuous values between 0 (air) and 1 (tissue). | ||
| + | Current field modeling techniques, including the one described in [2], do not | ||
| + | account for the shim fields that reduce the B0 inhomogeneity prior to fieldmap | ||
| + | acquisition. Therefore, in order to compare an estimated fieldmap to an acquired | ||
| + | one, the shim fields must added to the predicted fieldmaps. This is done by mod- | ||
| + | eling the shim fields using the set of first and second order spherical harmonic | ||
| + | basis functions. In addition, a global scaling of the predicted fieldmap must be | ||
| + | estimated since the model assumes the magnetic susceptibility throughout the | ||
| + | brain is constant, but this may not be accurate near | ||
| + | bone interfaces where both partial volume effects and mis-estimation of segmen- | ||
| + | tation values are most likely to occur. Furthermore, the perturbing fieldmaps are | ||
| + | calculated assuming a perfectly homogeneous B0 field, which cannot be achieved | ||
| + | in practice due to constraints on the hardware. The fieldmap scaling and shim | ||
| + | parameters can be obtained by least squares fitting to the acquired fieldmap. | ||
| + | Once these coefficients are known, the predicted fieldmap | ||
| + | with shim can be compared to the acquired fieldmap. | ||
| + | |||
| + | |||
| + | The results of the fieldmap estimation are shown in Fig 7. | ||
| + | The first column of Fig. 7 shows fieldmaps computed from the intensity-based segmentations, which | ||
| + | show significant differences relative to the acquired fieldmaps shown for each | ||
| + | subject in column 3. These are especially noticable in areas that have lower signal in MR, such as in the ventricles and major sulci. Fieldmap results from the | ||
| + | atlas-based segmentations are shown in the second column of Fig. 7 and show | ||
| + | improved agreement with acquired fieldmaps. Quantitative analysis of the absolute error in the B0 field between these images is given in the table in Fig. 7. | ||
| + | Since the bandwidth/pixel for the EPI data acquired in this study is 22.3 Hz, | ||
| + | 90% of the voxels in the atlas-based fieldmaps show subvoxel error. The mean | ||
| + | of these statistics across all five subjects is also shown for both the intensity | ||
| + | and atlas-based classifiers. The intensity classifier shows a slight improvement | ||
| + | over the results reported by Koch et al [3] for a single subject. The atlas-based | ||
| + | classifier out performs both the intensity and Koch methods. Paired t-tests comparing the means of the intensity and atlas-based results shows this improvement | ||
| + | is statistically significant (all p-values < 0.05). | ||
| + | {| | ||
| + | |[[Image:Fieldmaps.jpg|600px|thumb|Fig. 7. Fieldmap Estimation. Fieldmaps predicted from intensity-based segmentations show significant differences relative to acquired fieldmaps while those computed from atlas-based segmentations show improved agreement. The mean absolute difference in field between computed and acquired fieldmaps for all 5 subjects is given in the table above, as well as results reported by Koch [3] for a single subject. In the atlas-based results, 90 % of voxels show sub-voxel error (field differences < 22.3 Hz, the bandwidth/pixel).]] | ||
| + | |} | ||
| + | |||
| + | |||
| + | |||
| + | |||
| + | [1] Cusack, et al. NeuroImage 18:127-142. 2003. | ||
| + | |||
| + | [2] Jenkinson, et al. Magn Reson Med 52:471-477. 2004. | ||
| + | |||
| + | [3] Koch, et al. Phys Med Biol. 51(24):6381-402. 2006. | ||
| + | |||
| + | [4] Poynton, et al. MICCAI. 271-279, 2008. | ||
| + | |||
| + | [5] Zubal IG, et al. Med. Phys. 21, 299--302. 1994. | ||
| + | |||
| + | [6] Poynton, et al. MICCAI. (in press). 2009. | ||
= Key Investigators = | = Key Investigators = | ||
| − | *Clare Poynton, | + | * MIT: Clare Poynton, Polina Golland |
| + | * BWH/Harvard:Alex Golby, William (Sandy) Wells | ||
| + | * Oxford: Mark Jenkinson | ||
= Publications = | = Publications = | ||
| − | + | [http://www.na-mic.org/publications/pages/display?search=Projects%3AFieldmapFreeDistortionCorrection&submit=Search&words=all&title=checked&keywords=checked&authors=checked&abstract=checked&sponsors=checked&searchbytag=checked| NA-MIC Publications Database on Fieldmap-Free EPI Distortion Correction] | |
| − | |||
| − | |||
Latest revision as of 20:04, 11 May 2010
Home < Projects:FieldmapFreeDistortionCorrectionBack to NA-MIC Collaborations, MIT Algorithms
Fieldmap-Free EPI Distortion Correction
Echo-planar imaging (EPI) is one of the most widely used pulse sequences in functional magnetic resonance imaging (fMRI) due to its high temporal resolution. The ability to acquire an entire volume within seconds makes it a valuable, non-invasive tool for probing dynamic physiological processes such as the blood-oxygenation-level-dependent (BOLD) response. A significant limitation of EPI is its sensitivity to magnetic field inhomogeneity. Perturbations in the field result in signal loss and geometric distortion in EPI data. Previous studies have shown that correcting geometric distortion in functional images increases the accuracy of co-registration to structural MR. Precise anatomical localization of functional activation is especially important in single-subject studies (ie. pre-surgical evaluation) and in cases where the structural MR is used as a reference to sample the functional data (ie. cortical-surface-based analysis). Therefore, field inhomogeneity and distortion is a significant problem in fMRI. In this work, we describe a method for correcting the distortions present in echo planar images (EPI) and registering the EPI to structural MRI. A fieldmap is predicted from a tissue/air segmentation of the MRI using a perturbation method and subsequently used to unwarp the EPI data. Shim and other missing parameters are estimated by registration. We obtain results that are similar to those obtained using fieldmaps, however neither fieldmaps, nor knowledge of shim parameters is required.
Registration without Correction
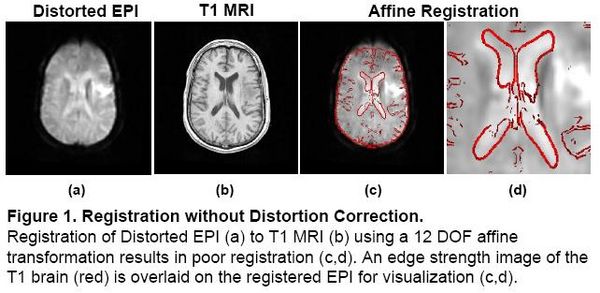
Localization of functional information relies on accurate registration of EPI and structural MR, which can be difficult due to EPI distortion caused by B0 field inhomogeneity. Correcting distortion using acquired Fieldmaps has been shown to improve registration [1], but Fieldmaps may not be available or may not be applicable if significant motion is present in the EPI, resulting in sub-optimal registration.
|
Problem 1: Segmentation
Magnetic field models exist to compute a Fieldmap from a Tissue/Air segmentation [2,3], but segmenting structural MR is difficult due to the similar intensities of bone and air. In the Fieldmap-Free method [4], T1 MRI was segmented using a trained classifier that computes the probability of tissue given MR intensity. CT data was used for training and validation only, allowing the trained classifier to be applied to data sets without CT.
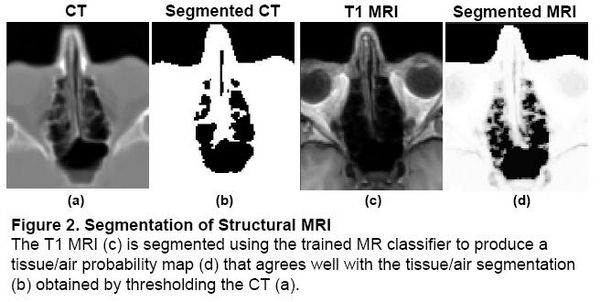
|
Problem 2: Shim Estimation
Existing magnetic field models do not account for the shim fields that reduce B0 field inhomogeniety prior to acquisition. Without this information, accurate unwarping is not possible. In this Method, a Fieldmap (without shim) was computed from the Segmented MR using the field model in [2]. Missing Shim Fields were modeled by spherical harmonic basis functions. Registration was used to search over shim parameters until optimal agreement between the EPI and structural MR was obtained.
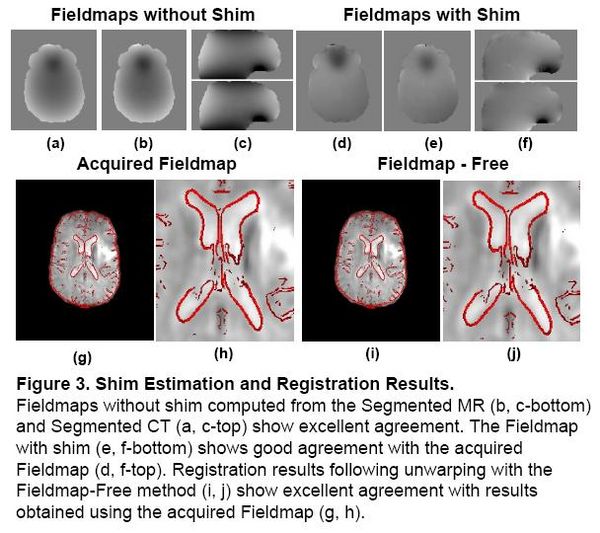
|
Atlas-Based Improved Prediction of Magnetic Field Inhomogeneity for Distortion Correction of EPI Data Motivation
In the Fieldmap-Free method described above, it was shown that tissue/air susceptibility models could be derived from structural MRI by using an intensity-based classifier trained with CT [4]. It was also shown that registration of the EPI and structural MR could be used to search over the unknown shim parameters allowing distortion correction of the EPI that agrees well with results obtained using acquired fieldmaps.
Variability in structural MR acquisitions, however, may limit the efficacy of an intensity-based classifier in cases where the MR intensity properties differ significantly from those of the training data. In [4], CT data sets with MR acquired on the same scanner as the subjects of interest could be used to train the classifier, but this may not be possible in many cases. Limited anatomical information below the brain may also prevent accurate estimation of the perturbing field. Therefore, obtaining more reliable susceptibility models from structural MR is critical for retrospective unwarping of EPI data sets that lack acquired fieldmaps. While previous results predicting fieldmaps from structural MR have shown good agreement with acquired fieldmaps, we hypothesized that improved segmentation methods would result in even greater accuracy.
Description
In this work, anatomical information from a set of 22 whole-head CT data sets is used to achieve improved, subject-specific segmentation of structural MR. A tissue/air atlas is constructed from the CT data to obtain priors on the probability of tissue or air at each location in the anatomy. The corresponding structural MR is used to train a classifier that segments the MR of the subject of interest and this is used as input to a first order perturbation field model to compute a subject-specific fieldmap. The method is evaluated by comparison of predicted fieldmaps and acquired fieldmaps. In addition, the MR classifier can be used to obtain probabilistic bone segmentations from structural MR that show promising agreement with segmented CT.
Results
Atlas Construction
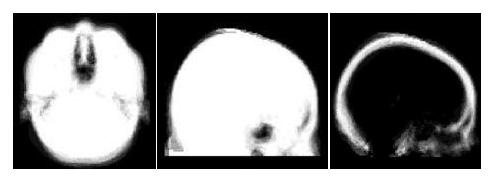
We obtained 22 datasets consisting of CT and MRI from 3 sources: the publicly available Retrospective Image Registration Evaluation (RIRE) database (17 neurosurgery patients), the Radiology department at Brigham and Women's Hospital (BWH) (4 neurosurgery patients) and the Zubal head phantom (1 subject) [5]. For each subject, the CT data was registered to its corresponding MR. The MR was registered to standard space and these transformations were then applied to the co-registered CT. Tissue/air labels were obtained by thresholding the CT data in standard space. Probabilistic tissue/air and air/bone atlases were then constructed [6] and are shown in Fig. 4 below.
Atlas-based Segmentation
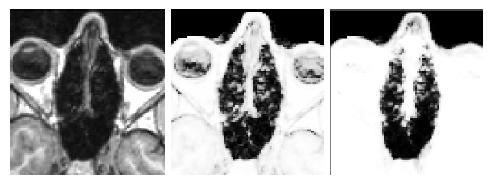
Structural MR was segmented using an MR classifier that incorporates spatially dependent prior information from the probabilistic atlas and MR intensity information (from the subject of interest) to obtain a subject-specific susceptibility model. The classifier was trained using the CT/MR training data described above, but applied to segment MR data acquired at a separate site. The accuracy of the segmentations was evaluated by comparing fieldmaps predicted from the atlas-based segmenter to acquired fieldmaps. The fieldmaps were also compared to those predicted using intensity information alone (ie. a spatially constant prior).
Results of atlas-based segmentation of structural MR is shown in Fig. 5 below.
T1 of the sinus region is shown on the left. The limitations of using the intensity
classifier to segment the MR is shown in the middle image. While the classifier produces reasonable results for many of the voxels in the sinuses,
voxels outside this region which are clearly soft tissue or
bone are mislabeled with values close to zero. In contrast, using the atlas-based
segmenter (right image) achieves similar results for the highly variable
subject-specific anatomy within the sinus region, while producing fewer errors
in the surrounding area.
Results of the segmentation of bone from structural MR for a representative subject is shown in Fig. 6. The
CT shown on the left can be easily thresholded to segment bone from air and
soft tissue. The results of using the intensity and atlas-
based classifiers are shown in the middle and right images, respectively. While the intensity classifier has some success in
segmenting MR into tissue/air classes, it is much less effective in segmenting
bone. Inspection of the the atlas-based segmentation, however, shows good general agreement with the CT, with a dice score of 0.780 for
this subject.
Fieldmap Estimation
Fieldmaps are predicted from the atlas and intensity-based segmentations using the perturbation field model described in [2]. In this model, a first order perturba- tion solution of Maxwell’s equations is calculated from a tissue/air susceptibility model, where each pixel takes continuous values between 0 (air) and 1 (tissue). Current field modeling techniques, including the one described in [2], do not account for the shim fields that reduce the B0 inhomogeneity prior to fieldmap acquisition. Therefore, in order to compare an estimated fieldmap to an acquired one, the shim fields must added to the predicted fieldmaps. This is done by mod- eling the shim fields using the set of first and second order spherical harmonic basis functions. In addition, a global scaling of the predicted fieldmap must be estimated since the model assumes the magnetic susceptibility throughout the brain is constant, but this may not be accurate near bone interfaces where both partial volume effects and mis-estimation of segmen- tation values are most likely to occur. Furthermore, the perturbing fieldmaps are calculated assuming a perfectly homogeneous B0 field, which cannot be achieved in practice due to constraints on the hardware. The fieldmap scaling and shim parameters can be obtained by least squares fitting to the acquired fieldmap. Once these coefficients are known, the predicted fieldmap with shim can be compared to the acquired fieldmap.
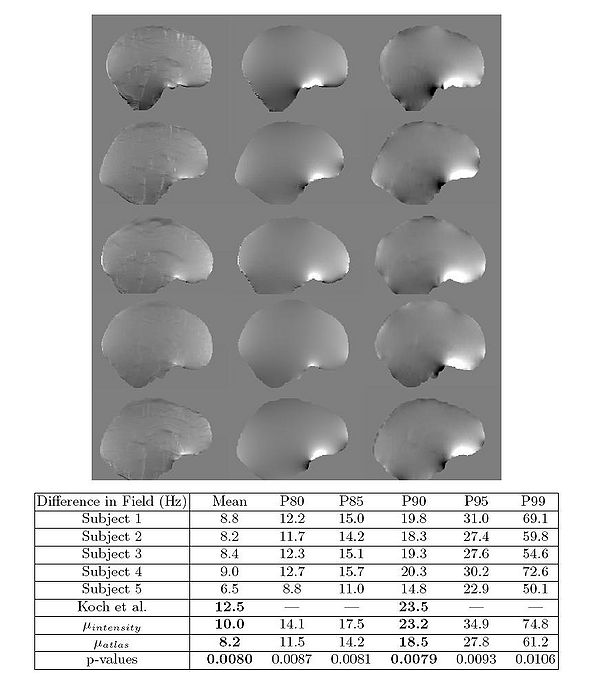
The results of the fieldmap estimation are shown in Fig 7.
The first column of Fig. 7 shows fieldmaps computed from the intensity-based segmentations, which
show significant differences relative to the acquired fieldmaps shown for each
subject in column 3. These are especially noticable in areas that have lower signal in MR, such as in the ventricles and major sulci. Fieldmap results from the
atlas-based segmentations are shown in the second column of Fig. 7 and show
improved agreement with acquired fieldmaps. Quantitative analysis of the absolute error in the B0 field between these images is given in the table in Fig. 7.
Since the bandwidth/pixel for the EPI data acquired in this study is 22.3 Hz,
90% of the voxels in the atlas-based fieldmaps show subvoxel error. The mean
of these statistics across all five subjects is also shown for both the intensity
and atlas-based classifiers. The intensity classifier shows a slight improvement
over the results reported by Koch et al [3] for a single subject. The atlas-based
classifier out performs both the intensity and Koch methods. Paired t-tests comparing the means of the intensity and atlas-based results shows this improvement
is statistically significant (all p-values < 0.05).
[1] Cusack, et al. NeuroImage 18:127-142. 2003.
[2] Jenkinson, et al. Magn Reson Med 52:471-477. 2004.
[3] Koch, et al. Phys Med Biol. 51(24):6381-402. 2006.
[4] Poynton, et al. MICCAI. 271-279, 2008.
[5] Zubal IG, et al. Med. Phys. 21, 299--302. 1994.
[6] Poynton, et al. MICCAI. (in press). 2009.
Key Investigators
- MIT: Clare Poynton, Polina Golland
- BWH/Harvard:Alex Golby, William (Sandy) Wells
- Oxford: Mark Jenkinson
Publications
NA-MIC Publications Database on Fieldmap-Free EPI Distortion Correction