Difference between revisions of "Projects:ConformalFlatteningRegistration"
| (9 intermediate revisions by 2 users not shown) | |||
| Line 1: | Line 1: | ||
| − | Back to [[NA-MIC_Internal_Collaborations:fMRIAnalysis|NA-MIC_Collaborations]], [[Algorithm: | + | Back to [[NA-MIC_Internal_Collaborations:fMRIAnalysis|NA-MIC_Collaborations]], [[Algorithm:Stony Brook|Stony Brook University Algorithms]] |
__NOTOC__ | __NOTOC__ | ||
= Conformal Flattening Registration = | = Conformal Flattening Registration = | ||
| Line 12: | Line 12: | ||
# The conformal mapping <span class="texhtml">''f''</span> is defined on the originla surface <span class="texhtml">Σ</span> as <math>\triangle f = (\frac{\partial}{\partial u} - i\frac{\partial}{\partial v})\delta_p</math>. In that <span class="texhtml">''u''</span> and <span class="texhtml">''v''</span> are the conformal coordinates defined on the surface and the <span class="texhtml">δ<sub>''p''</sub></span> is a Dirac function whose value is non-zero only at point <span class="texhtml">''p''</span>. By solving this partial differential equation the mapping <span class="texhtml">''f''</span> can be obtained. | # The conformal mapping <span class="texhtml">''f''</span> is defined on the originla surface <span class="texhtml">Σ</span> as <math>\triangle f = (\frac{\partial}{\partial u} - i\frac{\partial}{\partial v})\delta_p</math>. In that <span class="texhtml">''u''</span> and <span class="texhtml">''v''</span> are the conformal coordinates defined on the surface and the <span class="texhtml">δ<sub>''p''</sub></span> is a Dirac function whose value is non-zero only at point <span class="texhtml">''p''</span>. By solving this partial differential equation the mapping <span class="texhtml">''f''</span> can be obtained. | ||
| − | # To solve that equation on the discrete mesh representation of the surface, finite element method(FEM) is used. The problem is turned to solving a linear system <span class="texhtml">''D''''x'' = ''b''</span>. Since b is complex vector, the real and imaginary parts of the mapping <span class="texhtml">''f''</span> can be calculated separately by two linear system. | + | # To solve that equation on the discrete mesh representation of the surface, finite element method(FEM) is used. The problem is turned to solving a linear system <span class="texhtml">''D''.''x'' = ''b''</span>. Since b is complex vector, the real and imaginary parts of the mapping <span class="texhtml">''f''</span> can be calculated separately by two linear system. |
# Having the mapping <span class="texhtml">''f''</span>, the original surface can be mapped to a plane. | # Having the mapping <span class="texhtml">''f''</span>, the original surface can be mapped to a plane. | ||
# Further, the plane can be mapped to a sphere by the stereographic projection. | # Further, the plane can be mapped to a sphere by the stereographic projection. | ||
| Line 18: | Line 18: | ||
Also, in the work of [[Algorithm:GATech:Multiscale_Shape_Segmentation|Multiscale Shape Segmentation]], conformal flattening is used as the first step for remeshing the surface. | Also, in the work of [[Algorithm:GATech:Multiscale_Shape_Segmentation|Multiscale Shape Segmentation]], conformal flattening is used as the first step for remeshing the surface. | ||
| − | + | = Progress = | |
| + | The road to ITK and Slicer3: | ||
| − | + | == ITK == | |
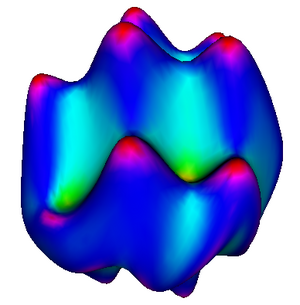
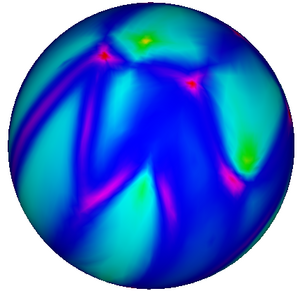
| + | The conformal flattening algorithm is now in ITK/Code/Review/itkConformalFlatteningMeshFilter.h/txx. The following figures show how the surfaces are mapped conformally to a sphere. | ||
| − | [[Image:Nice.PNG| | + | [[Image:Nice.PNG| | 300px ]] ===> [[Image:Nice-flat.PNG| 300px ]] |
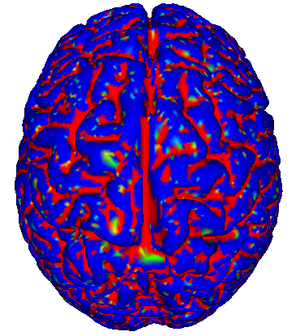
| − | [[Image:Brain.PNG| | + | [[Image:Brain.PNG | 300px ]] ===> [[Image:Brain-flat.PNG | 300px ]] |
| − | = | + | == Slicer3 module == |
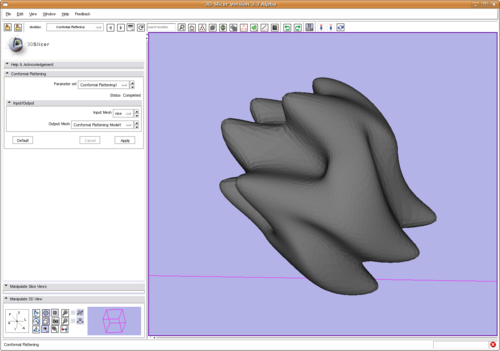
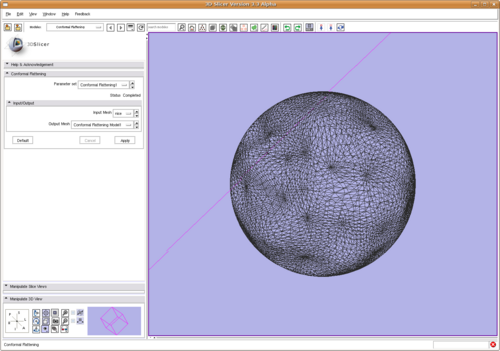
| − | + | During the project week 2008, it is further put into Slicer3 as a command line module. Below we show two screen shots of using it. | |
| − | [[Image:SlicerConformalFlatten.png| The mesh to be mapped to sphere. | | + | [[Image:SlicerConformalFlatten.png| The mesh to be mapped to sphere. | 500px]] |
| + | [[Image:SlicerConformalFlattenResult.png| The spherical image of the mesh. | 500px]] | ||
| − | + | = Acceleration = | |
| + | |||
| + | The major computation happens in the solution of the linear system using conjugate gradient method. This can be accelerated using the pre-conditioning technique. | ||
= Key Investigators = | = Key Investigators = | ||
| − | *Georgia Tech Algorithms: John Melonakos, | + | *Georgia Tech Algorithms: Yi Gao, John Melonakos, Allen Tannenbaum |
= Publications = | = Publications = | ||
| − | + | * [http://www.na-mic.org/publications/pages/display?search=ConformalFlatteningRegistration&submit=Search&words=all&title=checked&keywords=checked&authors=checked&abstract=checked&searchbytag=checked&sponsors=checked| NA-MIC Publications Database on Conformal Flattening (inactive)] | |
| − | |||
| − | *[http://www.na-mic.org/publications/pages/display?search=ConformalFlatteningRegistration&submit=Search&words=all&title=checked&keywords=checked&authors=checked&abstract=checked&searchbytag=checked&sponsors=checked| NA-MIC Publications Database] | ||
[[Category:fMRI]] [[Category:Registration]] | [[Category:fMRI]] [[Category:Registration]] | ||
Latest revision as of 00:57, 16 November 2013
Home < Projects:ConformalFlatteningRegistrationBack to NA-MIC_Collaborations, Stony Brook University Algorithms
Conformal Flattening Registration
The goal of this project is for better visualizing and computation of neural activity from fMRI brain imagery. Also, with this technique, shapes can be mapped to spheres for shape analysis, registration or other purposes. Our technique is based on conformal mappings which map genus-zero surface: in fMRI case cortical or other surfaces, onto a sphere in an angle preserving manner.
The explicit transform is obtained by solving a partial differential equation. Such transform will map the original surface to a plane(flattening) and then one can use classic stereographic transformation to map the plane to a sphere.
Description
The process of the algorithm is briefly given below:
- The conformal mapping f is defined on the originla surface Σ as [math]\triangle f = (\frac{\partial}{\partial u} - i\frac{\partial}{\partial v})\delta_p[/math]. In that u and v are the conformal coordinates defined on the surface and the δp is a Dirac function whose value is non-zero only at point p. By solving this partial differential equation the mapping f can be obtained.
- To solve that equation on the discrete mesh representation of the surface, finite element method(FEM) is used. The problem is turned to solving a linear system D.x = b. Since b is complex vector, the real and imaginary parts of the mapping f can be calculated separately by two linear system.
- Having the mapping f, the original surface can be mapped to a plane.
- Further, the plane can be mapped to a sphere by the stereographic projection.
Also, in the work of Multiscale Shape Segmentation, conformal flattening is used as the first step for remeshing the surface.
Progress
The road to ITK and Slicer3:
ITK
The conformal flattening algorithm is now in ITK/Code/Review/itkConformalFlatteningMeshFilter.h/txx. The following figures show how the surfaces are mapped conformally to a sphere.
Slicer3 module
During the project week 2008, it is further put into Slicer3 as a command line module. Below we show two screen shots of using it.
Acceleration
The major computation happens in the solution of the linear system using conjugate gradient method. This can be accelerated using the pre-conditioning technique.
Key Investigators
- Georgia Tech Algorithms: Yi Gao, John Melonakos, Allen Tannenbaum