Difference between revisions of "NA-MIC Internal Collaborations:StructuralImageAnalysis"
| (34 intermediate revisions by one other user not shown) | |||
| Line 6: | Line 6: | ||
{| cellpadding="10" style="text-align:left;" | {| cellpadding="10" style="text-align:left;" | ||
| − | | style="width:15%" | [[Image: | + | | style="width:15%" | [[Image:MITHippocampalSubfieldSegmentation.png|200px]] |
| style="width:85%" | | | style="width:85%" | | ||
| − | == [[ | + | == [[Projects:BayesianMRSegmentation| Bayesian Segmentation of MRI Images]] == |
| − | + | In this project we develop and validate a method for fully automated segmentation of the subfields of the hippocampus in ultra-high resolution in vivo MRI. [[Projects:HippocampalSubfieldSegmentation|More...]] | |
| − | <font color="red">'''New: '''</font> | + | <font color="red">'''New: '''</font> van Leemput K., Bakkour A., Benner T., Wiggins G., Wald L.L., Augustinack J., Dickerson B.C., Golland P., Fischl B. Automated segmentation of hippocampal subfields from ultra-high resolution in vivo MRI. Hippocampus. 2009 Jun;19(6):549-57. |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| + | van Leemput K. Encoding probabilistic brain atlases using Bayesian inference. IEEE Trans Med Imaging. 2009 Jun;28(6):822-37. | ||
|} | |} | ||
| − | |||
=== Image Registration === | === Image Registration === | ||
{| cellpadding="10" style="text-align:left;" | {| cellpadding="10" style="text-align:left;" | ||
| − | | style="width:15%" | [[Image: | + | | style="width:15%" | [[Image:Sulcaldepth.png|200px]] |
| style="width:85%" | | | style="width:85%" | | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
== [[Projects:CorticalCorrespondenceWithParticleSystem|Cortical Correspondence using Particle System]] == | == [[Projects:CorticalCorrespondenceWithParticleSystem|Cortical Correspondence using Particle System]] == | ||
| Line 67: | Line 28: | ||
In this project, we want to compute cortical correspondence on populations, using various features such as cortical structure, DTI connectivity, vascular structure, and functional data (fMRI). This presents a challenge because of the highly convoluted surface of the cortex, as well as because of the different properties of the data features we want to incorporate together. [[Projects:CorticalCorrespondenceWithParticleSystem|More...]] | In this project, we want to compute cortical correspondence on populations, using various features such as cortical structure, DTI connectivity, vascular structure, and functional data (fMRI). This presents a challenge because of the highly convoluted surface of the cortex, as well as because of the different properties of the data features we want to incorporate together. [[Projects:CorticalCorrespondenceWithParticleSystem|More...]] | ||
| − | <font color="red">'''New: '''</font> Oguz I, Niethammer M, Cates J, Whitaker R, Fletcher T, Vachet C, Styner M. | + | <font color="red">'''New: '''</font> Oguz I., Niethammer M., Cates J., Whitaker R., Fletcher T., Vachet C., Styner M. Cortical Correspondence with Probabilistic Fiber Connectivity. Inf Process Med Imaging. 2009;21:651-63. |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
|- | |- | ||
| Line 90: | Line 40: | ||
[[Projects:MultimodalAtlas|More...]] | [[Projects:MultimodalAtlas|More...]] | ||
| − | <font color="red">'''New: '''</font> | + | <font color="red">'''New: '''</font> Yeo B.T.T., Sabuncu M.R., Golland P., Fischl B. Task-Optimal Registration Cost Functions. Int Conf Med Image Comput Comput Assist Interv. 2009;12(Pt 1):1009-1017. |
| − | |||
|- | |- | ||
| − | | | [[Image: | + | | | [[Image:CoordinateChart.png|200px]] |
| | | | | | ||
| − | == [[Projects: | + | == [[Projects:SphericalDemons|Spherical Demons: Fast Surface Registration]] == |
| − | |||
| − | |||
| − | |||
| − | + | We present the fast Spherical Demons algorithm for registering two spherical images. By exploiting spherical vector spline interpolation theory, we show that a large class of regularizers for the modified demons objective function can be efficiently approximated on the sphere using convolution. Based on the one parameter subgroups of diffeomorphisms, [[Projects:SphericalDemons|More...]] | |
| − | |||
| − | = | + | <font color="red">'''New: '''</font> Yeo B.T.T., Sabuncu M.R., Vercauteren T., Ayache N., Fischl B., Golland P. Spherical Demons: Fast Surface Registration. Int Conf Med Image Comput Comput Assist Interv. 2008;11(Pt 1):745-753. |
| − | + | <font color="red">'''New: '''</font> Yeo B.T.T., Sabuncu M.R., Vercauteren T., Ayache N., Fischl B., Golland P. Spherical Demons: Fast Surface Registration. IEEE TMI, In Press. | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
|- | |- | ||
| − | | | [[Image: | + | | | [[Image:JointRegSeg.png|200px]] |
| | | | | | ||
| − | == [[Projects: | + | == [[Projects:RegistrationRegularization|Optimal Atlas Regularization in Image Segmentation]] == |
| − | + | We propose a unified framework for computing atlases from manually labeled data sets at various degrees of “sharpness” and the joint registration and segmentation of a new brain with these atlases. Using this framework, we investigate the tradeoff between warp regularization and image fidelity, i.e. the smoothness of the new subject warp and the sharpness of the atlas in a segmentation application. | |
| + | [[Projects:RegistrationRegularization|More...]] | ||
| − | <font color="red">'''New:'''</font> | + | <font color="red">'''New:'''</font> Yeo B.T.T., Sabuncu M.R., Desikan R., Fischl B., Golland P. Effects of Registration Regularization and Atlas Sharpness on Segmentation Accuracy. Med Image Anal. 2008 Oct;12(5):603-15. |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
|- | |- | ||
| − | | | | + | | | [[Image:Cbg-dtiatlas-tracts.png|200px]] |
| | | | | | ||
| − | == [[Projects: | + | == [[Projects:DTIPopulationAnalysis|Population Analysis from Deformable Registration]] == |
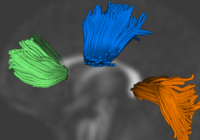
| − | + | Analysis of populations of diffusion images typically requires time-consuming manual segmentation of structures of interest to obtain correspondance for statistics. This project uses non-rigid registration of DTI images to produce a common coordinate system for hypothesis testing of diffusion properties. [[Projects:DTIPopulationAnalysis|More...]] | |
| − | | | + | <font color="red">'''New: '''</font> Goodlett C., Fletcher P.T., Gilmore J.H., Gerig G. Group Analysis of DTI Fiber Tract Statistics with Application to Neurodevelopment. Neuroimage. 2009 Mar;45(1 Suppl):S133-42. |
| + | |} | ||
| − | + | === Morphometric Measures and Shape Analysis === | |
| − | |||
| − | == | + | {| cellpadding="10" style="text-align:left;" |
| − | + | | style="width:15%" | [[Image:P1_small.png|200px|]] | |
| − | + | | style="width:85%" | | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | | | | ||
| − | == [[Projects: | + | == [[Projects:LabelSpace|Label Space: A Coupled Multi-Shape Representation]] == |
| − | + | Many techniques for multi-shape representation may often develop inaccuracies stemming from either approximations or inherent variation. Label space is an implicit representation that offers unbiased algebraic manipulation and natural expression of label uncertainty. We demonstrate smoothing and registration on multi-label brain MRI. [[Projects:LabelSpace|More...]] | |
| − | <font color="red">'''New: '''</font> J | + | <font color="red">'''New: '''</font> Malcolm J.G., Rathi Y., Shenton M.E., Tannenbaum A. Label Space: A Coupled Multi-shape Representation. Int Conf Med Image Comput Comput Assist Interv. 2008;11(Pt 2):416-424. |
|- | |- | ||
| Line 182: | Line 101: | ||
The UNC shape analysis is based on an analysis framework of objects with spherical topology, described mainly by sampled spherical harmonics SPHARM-PDM. The input of the shape analysis framework is a set of binary segmentations of a single brain structure, such as the hippocampus or caudate. These segmentations are converted into a shape description (SPHARM) with correspondence and analyzed via Hotelling T^2 two sample metric. [[Projects:ShapeAnalysisFrameworkUsingSPHARMPDM|More...]] | The UNC shape analysis is based on an analysis framework of objects with spherical topology, described mainly by sampled spherical harmonics SPHARM-PDM. The input of the shape analysis framework is a set of binary segmentations of a single brain structure, such as the hippocampus or caudate. These segmentations are converted into a shape description (SPHARM) with correspondence and analyzed via Hotelling T^2 two sample metric. [[Projects:ShapeAnalysisFrameworkUsingSPHARMPDM|More...]] | ||
| − | <font color="red">'''New: '''</font> | + | <font color="red">'''New: '''</font> Zhu H., Zhou H., Chen J., Li Y., Lieberman J., Styner M. Adjusted exponentially tilted likelihood with applications to brain morphology. Biometrics. 2009 Sep;65(3):919-27. |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | Levitt J.J., Styner M., Niethammer M., Bouix S., Koo M., Voglmaier M.M., Dickey C., Niznikiewicz M.A., Kikinis R., McCarley R.W., Shenton M.E. Shape abnormalities of caudate nucleus in schizotypal personality disorder. Schizophr Res. 2009 May;110(1-3):127-139. | |
| − | + | * Shape Analysis Toolkit available as part of UNC Neurolib open source ([http://www.ia.unc.edu/dev/download/shapeAnalysis download]). | |
| − | + | * Slicer 3 module for whole shape analysis pipeline in progress (data access via XNAT, processing via BatchMake and distributed computing using Condor) | |
|- | |- | ||
| Line 242: | Line 116: | ||
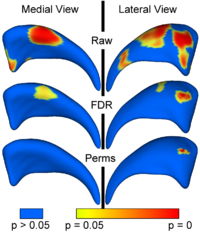
We have further developed a set of statistical testing methods that allow the analysis of local shape differences using the Hotelling T 2 two sample metric. Permutatioin tests are employed for the computation of statistical p-values, both raw and corrected for multiple comparisons. Resulting significance maps are easily visualized. Additional visualization of the group tests are provided via mean difference magnitude and vector maps, as well as maps of the group covariance information. Ongoing research focuses on incorporating covariates such as clinical scores into the testing scheme. [[Projects:LocalStatisticalAnalysisViaPermutationTests|More...]] | We have further developed a set of statistical testing methods that allow the analysis of local shape differences using the Hotelling T 2 two sample metric. Permutatioin tests are employed for the computation of statistical p-values, both raw and corrected for multiple comparisons. Resulting significance maps are easily visualized. Additional visualization of the group tests are provided via mean difference magnitude and vector maps, as well as maps of the group covariance information. Ongoing research focuses on incorporating covariates such as clinical scores into the testing scheme. [[Projects:LocalStatisticalAnalysisViaPermutationTests|More...]] | ||
| − | <font color="red">'''New: '''</font> | + | <font color="red">'''New: '''</font> Paniagua B., Styner M., Macenko M., Pantazis D., Niethammer M. Local Shape Analysis using MANCOVA. Insight Journal, 2009 July-December, http://hdl.handle.net/10380/3124 |
| − | * Available as part of Shape Analysis Toolset in UNC Neurolib open source ([http://www.ia.unc.edu/dev/download/shapeAnalysis download]). | + | * Available as part of Shape Analysis Toolset in UNC Neurolib open source ([http://www.ia.unc.edu/dev/download/shapeAnalysis download]) with MANCOVA testing. |
|- | |- | ||
| − | | | [[Image: | + | | | [[Image:Cbg-dtiatlas-tracts.png|200px]] |
| | | | | | ||
| − | |||
| − | + | == [[Projects:DTIPopulationAnalysis|Group Analysis of DTI Fiber Tracts]] == | |
| − | + | Analysis of populations of diffusion images typically requires time-consuming manual segmentation of structures of interest to obtain correspondance for statistics. This project uses non-rigid registration of DTI images to produce a common coordinate system for hypothesis testing of diffusion properties. [[Projects:DTIPopulationAnalysis|More...]] | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| + | <font color="red">'''New: '''</font> Goodlett C., Fletcher P.T., Gilmore J.H., Gerig G. Group Analysis of DTI Fiber Tract Statistics with Application to Neurodevelopment. Neuroimage. 2009 Mar;45(1 Suppl):S133-42. | ||
|} | |} | ||
Latest revision as of 13:08, 14 May 2010
Home < NA-MIC Internal Collaborations:StructuralImageAnalysisBack to NA-MIC Internal Collaborations
Structural Image Analysis
Image Segmentation
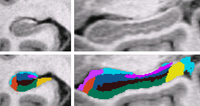
|
Bayesian Segmentation of MRI ImagesIn this project we develop and validate a method for fully automated segmentation of the subfields of the hippocampus in ultra-high resolution in vivo MRI. More... New: van Leemput K., Bakkour A., Benner T., Wiggins G., Wald L.L., Augustinack J., Dickerson B.C., Golland P., Fischl B. Automated segmentation of hippocampal subfields from ultra-high resolution in vivo MRI. Hippocampus. 2009 Jun;19(6):549-57. van Leemput K. Encoding probabilistic brain atlases using Bayesian inference. IEEE Trans Med Imaging. 2009 Jun;28(6):822-37. |
Image Registration
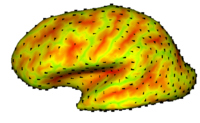
|
Cortical Correspondence using Particle SystemIn this project, we want to compute cortical correspondence on populations, using various features such as cortical structure, DTI connectivity, vascular structure, and functional data (fMRI). This presents a challenge because of the highly convoluted surface of the cortex, as well as because of the different properties of the data features we want to incorporate together. More... New: Oguz I., Niethammer M., Cates J., Whitaker R., Fletcher T., Vachet C., Styner M. Cortical Correspondence with Probabilistic Fiber Connectivity. Inf Process Med Imaging. 2009;21:651-63. |
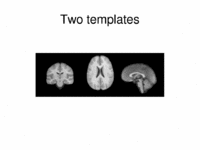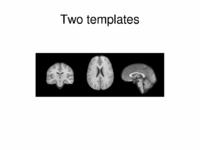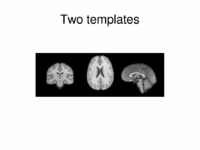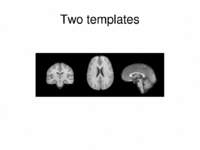
|
Multimodal AtlasIn this work, we propose and investigate an algorithm that jointly co-registers a collection of images while computing multiple templates. The algorithm, called iCluster, is used to compute multiple atlases for a given population. More... New: Yeo B.T.T., Sabuncu M.R., Golland P., Fischl B. Task-Optimal Registration Cost Functions. Int Conf Med Image Comput Comput Assist Interv. 2009;12(Pt 1):1009-1017. |
|
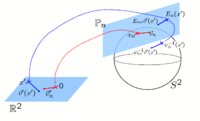
Spherical Demons: Fast Surface RegistrationWe present the fast Spherical Demons algorithm for registering two spherical images. By exploiting spherical vector spline interpolation theory, we show that a large class of regularizers for the modified demons objective function can be efficiently approximated on the sphere using convolution. Based on the one parameter subgroups of diffeomorphisms, More...
New: Yeo B.T.T., Sabuncu M.R., Vercauteren T., Ayache N., Fischl B., Golland P. Spherical Demons: Fast Surface Registration. IEEE TMI, In Press.
|
|
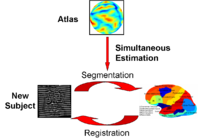
Optimal Atlas Regularization in Image SegmentationWe propose a unified framework for computing atlases from manually labeled data sets at various degrees of “sharpness” and the joint registration and segmentation of a new brain with these atlases. Using this framework, we investigate the tradeoff between warp regularization and image fidelity, i.e. the smoothness of the new subject warp and the sharpness of the atlas in a segmentation application. More... New: Yeo B.T.T., Sabuncu M.R., Desikan R., Fischl B., Golland P. Effects of Registration Regularization and Atlas Sharpness on Segmentation Accuracy. Med Image Anal. 2008 Oct;12(5):603-15. |
|
Population Analysis from Deformable RegistrationAnalysis of populations of diffusion images typically requires time-consuming manual segmentation of structures of interest to obtain correspondance for statistics. This project uses non-rigid registration of DTI images to produce a common coordinate system for hypothesis testing of diffusion properties. More... New: Goodlett C., Fletcher P.T., Gilmore J.H., Gerig G. Group Analysis of DTI Fiber Tract Statistics with Application to Neurodevelopment. Neuroimage. 2009 Mar;45(1 Suppl):S133-42. |
Morphometric Measures and Shape Analysis

|
Label Space: A Coupled Multi-Shape RepresentationMany techniques for multi-shape representation may often develop inaccuracies stemming from either approximations or inherent variation. Label space is an implicit representation that offers unbiased algebraic manipulation and natural expression of label uncertainty. We demonstrate smoothing and registration on multi-label brain MRI. More... New: Malcolm J.G., Rathi Y., Shenton M.E., Tannenbaum A. Label Space: A Coupled Multi-shape Representation. Int Conf Med Image Comput Comput Assist Interv. 2008;11(Pt 2):416-424. |

|
Shape Analysis Framework using SPHARM-PDMThe UNC shape analysis is based on an analysis framework of objects with spherical topology, described mainly by sampled spherical harmonics SPHARM-PDM. The input of the shape analysis framework is a set of binary segmentations of a single brain structure, such as the hippocampus or caudate. These segmentations are converted into a shape description (SPHARM) with correspondence and analyzed via Hotelling T^2 two sample metric. More... New: Zhu H., Zhou H., Chen J., Li Y., Lieberman J., Styner M. Adjusted exponentially tilted likelihood with applications to brain morphology. Biometrics. 2009 Sep;65(3):919-27. Levitt J.J., Styner M., Niethammer M., Bouix S., Koo M., Voglmaier M.M., Dickey C., Niznikiewicz M.A., Kikinis R., McCarley R.W., Shenton M.E. Shape abnormalities of caudate nucleus in schizotypal personality disorder. Schizophr Res. 2009 May;110(1-3):127-139.
|
|
Local Statistical Analysis via Permutation TestsWe have further developed a set of statistical testing methods that allow the analysis of local shape differences using the Hotelling T 2 two sample metric. Permutatioin tests are employed for the computation of statistical p-values, both raw and corrected for multiple comparisons. Resulting significance maps are easily visualized. Additional visualization of the group tests are provided via mean difference magnitude and vector maps, as well as maps of the group covariance information. Ongoing research focuses on incorporating covariates such as clinical scores into the testing scheme. More... New: Paniagua B., Styner M., Macenko M., Pantazis D., Niethammer M. Local Shape Analysis using MANCOVA. Insight Journal, 2009 July-December, http://hdl.handle.net/10380/3124
|

|
Group Analysis of DTI Fiber TractsAnalysis of populations of diffusion images typically requires time-consuming manual segmentation of structures of interest to obtain correspondance for statistics. This project uses non-rigid registration of DTI images to produce a common coordinate system for hypothesis testing of diffusion properties. More... New: Goodlett C., Fletcher P.T., Gilmore J.H., Gerig G. Group Analysis of DTI Fiber Tract Statistics with Application to Neurodevelopment. Neuroimage. 2009 Mar;45(1 Suppl):S133-42. |