Difference between revisions of "Projects:BrainManifold"
m (Stub) |
|||
| (5 intermediate revisions by 2 users not shown) | |||
| Line 2: | Line 2: | ||
__NOTOC__ | __NOTOC__ | ||
= Brain Manifold Learning = | = Brain Manifold Learning = | ||
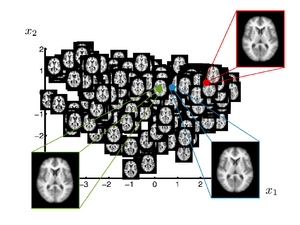
| + | [[Image:sgerber_brainmanifold_oasis_manifold.png|thumb|300px|Manifold learned from OASIS database. The image shows a 2-dimensional parametrization of the database. The green, red and blue are the mean, median and mode images computed using the manifold representation]] | ||
| − | + | This work investigates the use of manifold learning approaches in the context of brain population analysis. The goal is to construct a manifold model from a set of brain images that captures variability in shape, a parametrization of the shape space. | |
| − | + | Such a manifold model is interesting in several ways | |
| − | + | * The low dimensional parametrization simplifies statistical analysis of populations. | |
| − | + | * Applications to searching and browsing large database | |
| − | + | * The manifold represents a localized Atlas. Alternative to template based applications, for example as a segmentation prior. | |
| − | + | * Aid in clinical diagnosis. Different regions on the manifold can indicate different pathologies. | |
= Description = | = Description = | ||
| − | + | In many neuroimage applications a summary or representation of a population of brain images is needed. A common approach is to build a template, or atlas, that represents a population. Recent work introduced clustering based approaches, which in a data driven fashion, compute multiple templates Each template represents a part of the population. In a different direction, researcher proposed kernel-based regression of brain images with respect to an underlying parameter. This yields a continuous curve in the space of brain images that estimates the conditional expectation of a brain image given the parameter. A natural question that arises based on these investigations is can the space spanned by a set of brain images be approximated by a low-dimensional manifold? In other words, how effectively can a low-dimensional, nonlinear model represent the variability in brain anatomy. | |
= Key Investigators = | = Key Investigators = | ||
| Line 19: | Line 20: | ||
= Publications = | = Publications = | ||
| + | '' In Print '' | ||
| + | ''Published in MICCAI and ICCV'' | ||
| + | * [http://www.cs.utah.edu/~sgerber/research/ Manifold Learning Research Page] | ||
| + | * [http://www.na-mic.org/publications/pages/display?search=BrainManifold&submit=Search&words=all&title=checked&keywords=checked&authors=checked&abstract=checked&sponsors=checked&searchbytag=checked| NA-MIC Publications Database on Brain Manifold Learning] | ||
| + | |||
| + | '' In Press '' | ||
| + | |||
| + | * S Gerber, T Tasdizen, R Whitaker, Dimensionality Reduction and Principal Surfaces via Kernel Map, ICCV 2009 | ||
| + | * S Gerber, T Tasdizen, S Joshi, R Whitaker, On the Manifold Structure of the Space of Brain Images, MICCAI 2009 | ||
| − | + | [[Category:Statistics]] [[Category:Registration]] | |
Latest revision as of 20:26, 11 May 2010
Home < Projects:BrainManifoldBack to Utah Algorithms
Brain Manifold Learning
This work investigates the use of manifold learning approaches in the context of brain population analysis. The goal is to construct a manifold model from a set of brain images that captures variability in shape, a parametrization of the shape space. Such a manifold model is interesting in several ways
- The low dimensional parametrization simplifies statistical analysis of populations.
- Applications to searching and browsing large database
- The manifold represents a localized Atlas. Alternative to template based applications, for example as a segmentation prior.
- Aid in clinical diagnosis. Different regions on the manifold can indicate different pathologies.
Description
In many neuroimage applications a summary or representation of a population of brain images is needed. A common approach is to build a template, or atlas, that represents a population. Recent work introduced clustering based approaches, which in a data driven fashion, compute multiple templates Each template represents a part of the population. In a different direction, researcher proposed kernel-based regression of brain images with respect to an underlying parameter. This yields a continuous curve in the space of brain images that estimates the conditional expectation of a brain image given the parameter. A natural question that arises based on these investigations is can the space spanned by a set of brain images be approximated by a low-dimensional manifold? In other words, how effectively can a low-dimensional, nonlinear model represent the variability in brain anatomy.
Key Investigators
- Utah: Samuel Gerber, Tolga Tasdizen, Sarang Joshi, Tom Fletcher, Ross Whitaker
Publications
In Print Published in MICCAI and ICCV
In Press
- S Gerber, T Tasdizen, R Whitaker, Dimensionality Reduction and Principal Surfaces via Kernel Map, ICCV 2009
- S Gerber, T Tasdizen, S Joshi, R Whitaker, On the Manifold Structure of the Space of Brain Images, MICCAI 2009