Projects:BrainManifold

Back to Utah Algorithms

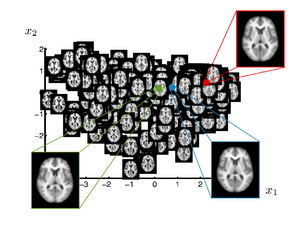
Brain Manifold Learning

Manifold learned from OASIS database. The image shows a 2-dimensional parametrization of the database. The green, red and blue are the mean, median and mode images computed using the manifold representation

This work investigates the use of manifold learning approaches in the context of brain population analysis. The goal is to construct a manifold model from a set of brain images that captures variability in shape, a parametrization of the shape space. Such a manifold model is interesting in several ways

• The low dimensional parametrization simplifies statistical analysis of populations.
• Applications to searching and browsing large database
• The manifold represents a localized Atlas. Alternative to template based applications, for example as a segmentation prior.
• Aid in clinical diagnosis. Different regions on the manifold can indicate different pathologies.

Description

In many neuroimage applications a summary or representation of a population of brain images is needed. A common approach is to build a template, or atlas, that represents a population. Recent work introduced clustering based approaches, which in a data driven fashion, compute multiple templates Each template represents a part of the population. In a different direction, researcher proposed kernel-based regression of brain images with respect to an underlying parameter. This yields a continuous curve in the space of brain images that estimates the conditional expectation of a brain image given the parameter. A natural question that arises based on these investigations is can the space spanned by a set of brain images be approximated by a low-dimensional manifold? In other words, how effectively can a low-dimensional, nonlinear model represent the variability in brain anatomy.

Key Investigators

• Utah: Samuel Gerber, Tolga Tasdizen, Sarang Joshi, Tom Fletcher, Ross Whitaker

Publications

In Print Published in MICCAI and ICCV

• Manifold Learning Research Page
• NA-MIC Publications Database on Brain Manifold Learning

In Press

• S Gerber, T Tasdizen, R Whitaker, Dimensionality Reduction and Principal Surfaces via Kernel Map, ICCV 2009
• S Gerber, T Tasdizen, S Joshi, R Whitaker, On the Manifold Structure of the Space of Brain Images, MICCAI 2009