Difference between revisions of "Projects:WhiteMatterGeometryDTGradients"
| (4 intermediate revisions by 3 users not shown) | |||
| Line 27: | Line 27: | ||
= Publications = | = Publications = | ||
| − | * | + | * Savadjiev P., Kindlmann G.L., Bouix S., Shenton M.E., Westin C-F. Local White Matter Geometry from Diffusion Tensor Gradients. Neuroimage. 2010 Febr 15;49(4):3175-3186. [http://pnl.bwh.harvard.edu/pub/papers_html/SavadjievNeuroImage10.html (see here for the reference)]. |
| − | |||
[[Category:Shape Analysis]] [[Category:Schizophrenia]] | [[Category:Shape Analysis]] [[Category:Schizophrenia]] | ||
Latest revision as of 13:44, 14 May 2010
Home < Projects:WhiteMatterGeometryDTGradientsLocal white matter geometry from diffusion tensor gradients
We introduce a mathematical framework for computing geometrical properties of white matter fibres directly from diffusion tensor fields. The key idea is to isolate the portion of the gradient of the tensor field corresponding to local variation in tensor orientation, and to project it onto a coordinate frame of tensor eigenvectors. The resulting eigenframe-centered representation then makes it possible to define scalar indices (or measures) that describe the local white matter geometry directly from the diffusion tensor field and its gradient, without requiring prior tractography. We derive new scalar indices of (1) fibre dispersion and (2) fibre curving, and we demonstrate them on synthetic and in vivo data. Finally, we illustrate their applicability to a group study on schizophrenia.
Description
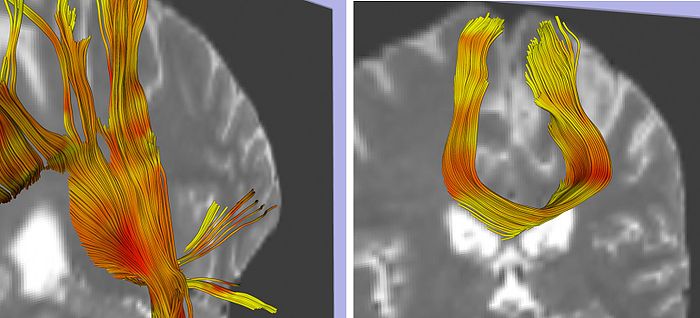
In addition to what can be learned about white matter structure from measures of individual tensor properties, such as FA, the information found in patterns of tensors and their differential structure may also provide insights into tissue organisation, structure and function. With this idea in mind, a method for DTI processing was recently developed (Savadjiev et al., 2010) and is under continuing investigation. The method introduces two quantitative measures of local tract geometry. The first is a fiber Dispersion Index (DI), measuring the extent to which the fibers deviate from being parallel (e.g. in the case of a fanning), and the second is a fiber Curving Index (CI), measuring the extent to which the fibers curve (Savadjiev et al., 2010). These indices are based on a mathematical framework that computes local variation in tensor orientation, from the gradient of the diffusion tensor field. Since they are defined in terms of tensor field derivatives, they integrate information from a neighbourhood of voxels, which is in contrast to traditional metrics such as FA. At the same time, white matter geometry is computed based on information intrinsic to the data, instead of requiring prior tractography (as in the standard methods in the literature), which makes the approach independent from potential tractography errors. The behaviour of the indices is illustrated in the figure below. For visualization purposes only, standard streamline tractography was run and colored with the pre-computed indices, so that red indicates a high index value, and yellow indicates a low index value. Note how DI captures the fanning of fibres passing through the internal capsule (left). The curving index CI is also consistent with the known geometry of the corpus callosum fibers, as illustrated in (right). In addition to this type of qualitative validation in vivo, the indices have also been successfully validated on synthetic data (Savadijev et al., 2010).
In current and future work, these indices will be applied to research in schizophrenia. A preliminary quantitative study on schizophrenia has already been reported (Savadijev et al., 2010). These measures are specifically tuned to isolate fiber geometry information from DTI data, which is not the case with traditional metrics such as FA, which can be influenced by a variety of factors that are not completely understood yet. Thus, we intend to use these measures in order to estimate the fraction of DTI changes related specifically to changes in white matter architecture, which could be then related to abnormalities in schizophrenia.
Key Investigators
- Brigham & Women's Hospital: Peter Savadjiev, Sylvain Bouix, Marek Kubicki, Martha E. Shenton, Carl-Fredrik Westin.
- University of Chicago: Gordon L. Kindlmann.
Publications
- Savadjiev P., Kindlmann G.L., Bouix S., Shenton M.E., Westin C-F. Local White Matter Geometry from Diffusion Tensor Gradients. Neuroimage. 2010 Febr 15;49(4):3175-3186. (see here for the reference).