Difference between revisions of "Projects:MultiTensorTractography"
| (2 intermediate revisions by 2 users not shown) | |||
| Line 3: | Line 3: | ||
We describe a unified framework to simultaneously estimate multiple fibers at | We describe a unified framework to simultaneously estimate multiple fibers at | ||
each location and perform tractography. Existing techniques estimate the local fiber orientation at each voxel | each location and perform tractography. Existing techniques estimate the local fiber orientation at each voxel | ||
| − | independently | + | independently. Consequently, there is no running knowledge of confidence in the |
| − | estimated fiber model. We formulate fiber tracking as recursive estimation: | + | estimated fiber model. We formulate fiber tracking as a recursive estimation: At each step of tracing |
the fiber, the current estimate is guided by the previous. | the fiber, the current estimate is guided by the previous. | ||
To do this we model the signal as either a weighted mixture of Gaussian tensors or | To do this we model the signal as either a weighted mixture of Gaussian tensors or | ||
Watson directional functions and | Watson directional functions and | ||
| − | perform tractography within a filter framework. | + | perform tractography within a filter framework. Starting from a seed point, the |
fiber is traced to its termination using an unscented Kalman filter to | fiber is traced to its termination using an unscented Kalman filter to | ||
simultaneously fit the local model and propagate in the most consistent | simultaneously fit the local model and propagate in the most consistent | ||
| − | direction. Further, we modify the Kalman filter to enforce model, i.e., positive eigenvalues and convex weights. Despite the | + | direction. Further, we modify the Kalman filter to enforce the model, i.e., positive eigenvalues and convex weights. Despite the |
presence of noise and uncertainty, this provides a causal estimate of the | presence of noise and uncertainty, this provides a causal estimate of the | ||
local structure at each point along the fiber. | local structure at each point along the fiber. | ||
| Line 18: | Line 18: | ||
Synthetic experiments demonstrate that this approach significantly improves | Synthetic experiments demonstrate that this approach significantly improves | ||
the angular resolution at crossings and branchings while consistently | the angular resolution at crossings and branchings while consistently | ||
| − | estimating the mixture weights. | + | estimating the mixture weights. ''In vivo'' experiments confirm the |
ability to trace out fibers in areas known to contain such crossing and | ability to trace out fibers in areas known to contain such crossing and | ||
branching while providing inherent path regularization. | branching while providing inherent path regularization. | ||
| Line 35: | Line 35: | ||
* J. Malcolm, M. E. Shenton, Y. Rathi. Two-Tensor Tractography Using a Constrained Filter. MICCAI, Pages 894-902, 2009 [http://pnl.bwh.harvard.edu/pub/papers_html/Malcolm-MICCAI2009.html (see here for the reference)]. | * J. Malcolm, M. E. Shenton, Y. Rathi. Two-Tensor Tractography Using a Constrained Filter. MICCAI, Pages 894-902, 2009 [http://pnl.bwh.harvard.edu/pub/papers_html/Malcolm-MICCAI2009.html (see here for the reference)]. | ||
| − | * J. Malcolm, O. Michailovich, S. Bouix, C.F. Westin, M. E. Shenton, Y. Rathi A filtered approach to neural tractography using the Watson directional function. Med Image Analysis, Volume 14, Pages 58-69 2010 [http://pnl.bwh.harvard.edu/pub/papers_html/MalcolmMedImage10.html (see here for the reference)] | + | * J. Malcolm, M. Kubicki, M. E. Shenton, Y. Rathi. The effect of local fiber model on population studies. Workshop on Diffusion modeling (MICCAI), Pages 33-40, 2009 [http://jgmalcolm.com/ (see here for the reference)]. |
| + | |||
| + | * J. Malcolm, O. Michailovich, S. Bouix, C.F. Westin, M. E. Shenton, Y. Rathi A filtered approach to neural tractography using the Watson directional function. Med Image Analysis, Volume 14, Pages 58-69 2010 [http://pnl.bwh.harvard.edu/pub/papers_html/MalcolmMedImage10.html (see here for the reference)] | ||
Latest revision as of 10:58, 14 May 2010
Home < Projects:MultiTensorTractographyMulti Tensor Tractography
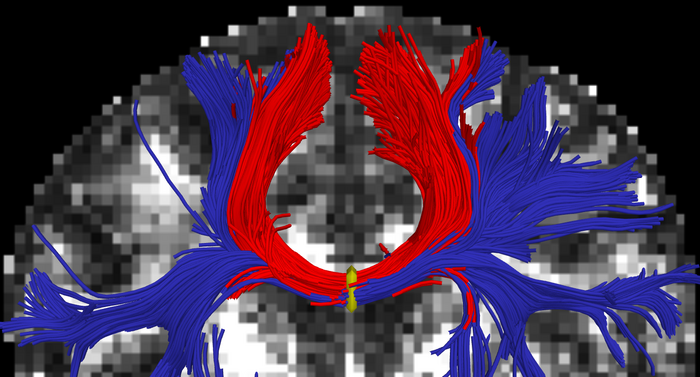
We describe a unified framework to simultaneously estimate multiple fibers at each location and perform tractography. Existing techniques estimate the local fiber orientation at each voxel independently. Consequently, there is no running knowledge of confidence in the estimated fiber model. We formulate fiber tracking as a recursive estimation: At each step of tracing the fiber, the current estimate is guided by the previous.
To do this we model the signal as either a weighted mixture of Gaussian tensors or Watson directional functions and perform tractography within a filter framework. Starting from a seed point, the fiber is traced to its termination using an unscented Kalman filter to simultaneously fit the local model and propagate in the most consistent direction. Further, we modify the Kalman filter to enforce the model, i.e., positive eigenvalues and convex weights. Despite the presence of noise and uncertainty, this provides a causal estimate of the local structure at each point along the fiber.
Synthetic experiments demonstrate that this approach significantly improves the angular resolution at crossings and branchings while consistently estimating the mixture weights. In vivo experiments confirm the ability to trace out fibers in areas known to contain such crossing and branching while providing inherent path regularization.
Key Investigators
- Brigham & Women's Hospital: Y. Rathi, J. Malcolm, Sylvain Bouix, Marek Kubicki, Martha E. Shenton, Carl-Fredrik Westin.
- University of Waterloo: O. Michailovich
Publications
- J. Malcolm, M. E. Shenton, Y. Rathi. Neural tractography using an unscented Kalman filter. Inf Process Med Imaging,Volume 21, Pages 126-138, 2009 (see here for the reference).
- J. Malcolm, M. E. Shenton, Y. Rathi. Two-Tensor Tractography Using a Constrained Filter. MICCAI, Pages 894-902, 2009 (see here for the reference).
- J. Malcolm, M. Kubicki, M. E. Shenton, Y. Rathi. The effect of local fiber model on population studies. Workshop on Diffusion modeling (MICCAI), Pages 33-40, 2009 (see here for the reference).
- J. Malcolm, O. Michailovich, S. Bouix, C.F. Westin, M. E. Shenton, Y. Rathi A filtered approach to neural tractography using the Watson directional function. Med Image Analysis, Volume 14, Pages 58-69 2010 (see here for the reference)