Difference between revisions of "Projects:ConnectivityAtlas"
| (18 intermediate revisions by one other user not shown) | |||
| Line 1: | Line 1: | ||
Back to [[NA-MIC_Internal_Collaborations:StructuralImageAnalysis|NA-MIC Collaborations]], [[Algorithm:MIT|MIT Algorithms]], | Back to [[NA-MIC_Internal_Collaborations:StructuralImageAnalysis|NA-MIC Collaborations]], [[Algorithm:MIT|MIT Algorithms]], | ||
__NOTOC__ | __NOTOC__ | ||
| − | = | + | = Building an atlas of functional connectivity patterns = |
| − | this and | + | |
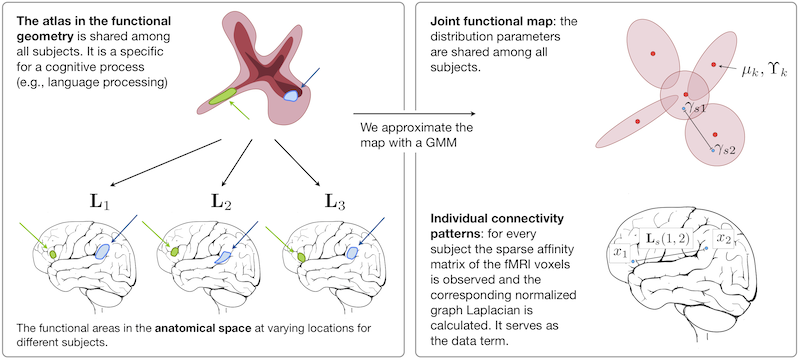
| + | We construct an atlas that captures functional connectivity characteristics of a cognitive process from a population of individuals. The functional connectivity is encoded in a low-dimensional embedding space derived from a diffusion process on a graph that represents correlations of fMRI time courses. The atlas is represented by a common prior distribution for the embedded fMRI signals of all subjects. The atlas is not directly coupled to the anatomical space, and can represent functional networks that are variable in their spatial distribution. We derive an algorithm for fitting this generative model to the observed data in a population. Our results in a language fMRI study demonstrate that the method identifies coherent and functionally equivalent regions across subjects. | ||
= Description = | = Description = | ||
| − | We | + | |
| + | We propose a different approach to characterize functional networks in a population of individuals. We do not assume a tight coupling between anatomical location and function, but view functional signals as the basis of a descriptive map that represents the global connectivity pattern during a specific cognitive process. We develop a representation of those networks based on manifold learning techniques and show how we can learn an <em>atlas</em> from a population of subjects performing the same task. Our main assumption is that the connectivity pattern associated with a functional process is consistent across individuals. Accordingly, we construct a generative model (the atlas) for these connectivity patterns that describes the common structures within the population. | ||
| + | |||
| + | The clinical goal of this work is to provide additional evidence for localization of functional areas. A robust localization approach is important for neurosurgical planning if individual activations are weak or reorganization has happened due to pathologies such as tumor growth. Furthermore the method provides a basis for understanding the mechanisms underlying formation and reorganization in the cerebral system. | ||
| + | [[File:ModelScheme_revision_2.png]] | ||
| + | '''''Fig.1''' Overview of the approach.'' | ||
== Experiments == | == Experiments == | ||
| − | + | We demonstrate the method on a set of six healthy control subjects. The language task (antonym generation) block design was 5min 10s long, starting with a 10s pre-stimulus period. Eight task and seven rest blocks, 20s each, alternated in the design. For each subject, an anatomical T1 MRI scan was acquired and registered to the functional data. Grey matter was segmented with FSL on the T1 data. The grey matter labels were transferred to the co-registered fMRI volumes, and computation was restricted to grey matter. | |
| + | |||
| + | We first apply clustering to signals from individual subjects separately to find subject-specific cluster assignments. We then apply clustering to signals combined from ''all'' subjects to construct the corresponding group-wise cluster assignments. Likewise, we cluster the diffusion map coordinates separately in each subject to obtain subject-specific assignments. We cluster the diffusion map coordinates of all subjects aligned to the first subject linearly, and the joint atlas. | ||
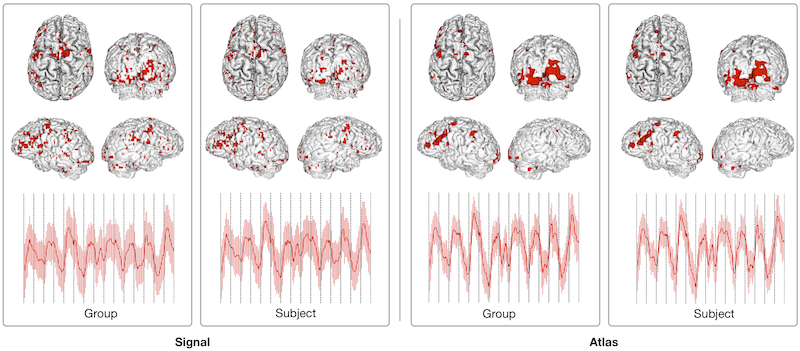
| + | Fig.2 shows top ranked clusters projected back onto the cortical surface for signal clustering, and for diffusion map clustering. | ||
| − | + | [[File:SurfaceFigure_revision.png]] | |
| − | [ | ||
| − | |||
| − | + | '''''Fig.2''' A comparison of the top ranked cluster when clustering in the signal space (left), and the joint atlas (right). For each clustering, we show the population level clustering on the left, and the individual clustering on the right. Below the average fMRI signal of the top ranked cluster is plotted. It is dominated by the language paradigm.'' | |
| − | |||
| − | + | == Conclusion == | |
| − | |||
| − | + | We learn an atlas of the functional connectivity structure that emerges during a cognitive process from a group of individuals. The atlas is a group-wise generative model that describes the fMRI responses of all subjects in the embedding space. The embedding space is a low dimensional representation of fMRI time courses that encodes the functional connectivity patterns within each subject. Future work will focus on the application of the framework to the study of reorganization processes. | |
= Key Investigators = | = Key Investigators = | ||
| Line 31: | Line 36: | ||
*MIT: Georg Langs, Andy Sweet, Danial Lashkari, Polina Golland | *MIT: Georg Langs, Andy Sweet, Danial Lashkari, Polina Golland | ||
*Harvard: Yanmei Tie, Laura Rigolo, Alexandra Golby | *Harvard: Yanmei Tie, Laura Rigolo, Alexandra Golby | ||
| − | |||
= Publications = | = Publications = | ||
| − | [http://www.na-mic.org/publications/pages/display?search=Projects% | + | [http://www.na-mic.org/publications/pages/display?search=Projects%3AConnectivityAtlas&submit=Search&words=all&title=checked&keywords=checked&authors=checked&abstract=checked&sponsors=checked&searchbytag=checked| NA-MIC Publications Database on Atlas of Functional Connectivity] |
Latest revision as of 17:52, 28 October 2011
Home < Projects:ConnectivityAtlasBack to NA-MIC Collaborations, MIT Algorithms,
Building an atlas of functional connectivity patterns
We construct an atlas that captures functional connectivity characteristics of a cognitive process from a population of individuals. The functional connectivity is encoded in a low-dimensional embedding space derived from a diffusion process on a graph that represents correlations of fMRI time courses. The atlas is represented by a common prior distribution for the embedded fMRI signals of all subjects. The atlas is not directly coupled to the anatomical space, and can represent functional networks that are variable in their spatial distribution. We derive an algorithm for fitting this generative model to the observed data in a population. Our results in a language fMRI study demonstrate that the method identifies coherent and functionally equivalent regions across subjects.
Description
We propose a different approach to characterize functional networks in a population of individuals. We do not assume a tight coupling between anatomical location and function, but view functional signals as the basis of a descriptive map that represents the global connectivity pattern during a specific cognitive process. We develop a representation of those networks based on manifold learning techniques and show how we can learn an atlas from a population of subjects performing the same task. Our main assumption is that the connectivity pattern associated with a functional process is consistent across individuals. Accordingly, we construct a generative model (the atlas) for these connectivity patterns that describes the common structures within the population.
The clinical goal of this work is to provide additional evidence for localization of functional areas. A robust localization approach is important for neurosurgical planning if individual activations are weak or reorganization has happened due to pathologies such as tumor growth. Furthermore the method provides a basis for understanding the mechanisms underlying formation and reorganization in the cerebral system.
Fig.1 Overview of the approach.
Experiments
We demonstrate the method on a set of six healthy control subjects. The language task (antonym generation) block design was 5min 10s long, starting with a 10s pre-stimulus period. Eight task and seven rest blocks, 20s each, alternated in the design. For each subject, an anatomical T1 MRI scan was acquired and registered to the functional data. Grey matter was segmented with FSL on the T1 data. The grey matter labels were transferred to the co-registered fMRI volumes, and computation was restricted to grey matter.
We first apply clustering to signals from individual subjects separately to find subject-specific cluster assignments. We then apply clustering to signals combined from all subjects to construct the corresponding group-wise cluster assignments. Likewise, we cluster the diffusion map coordinates separately in each subject to obtain subject-specific assignments. We cluster the diffusion map coordinates of all subjects aligned to the first subject linearly, and the joint atlas.
Fig.2 shows top ranked clusters projected back onto the cortical surface for signal clustering, and for diffusion map clustering.
Fig.2 A comparison of the top ranked cluster when clustering in the signal space (left), and the joint atlas (right). For each clustering, we show the population level clustering on the left, and the individual clustering on the right. Below the average fMRI signal of the top ranked cluster is plotted. It is dominated by the language paradigm.
Conclusion
We learn an atlas of the functional connectivity structure that emerges during a cognitive process from a group of individuals. The atlas is a group-wise generative model that describes the fMRI responses of all subjects in the embedding space. The embedding space is a low dimensional representation of fMRI time courses that encodes the functional connectivity patterns within each subject. Future work will focus on the application of the framework to the study of reorganization processes.
Key Investigators
- MIT: Georg Langs, Andy Sweet, Danial Lashkari, Polina Golland
- Harvard: Yanmei Tie, Laura Rigolo, Alexandra Golby
Publications
NA-MIC Publications Database on Atlas of Functional Connectivity