Difference between revisions of "Projects:DTIClustering"
| (32 intermediate revisions by 5 users not shown) | |||
| Line 1: | Line 1: | ||
| − | = | + | Back to [[NA-MIC_Internal_Collaborations:DiffusionImageAnalysis|NA-MIC Collaborations]], [[Algorithm:MIT|MIT Algorithms]], [[DBP1:Harvard|Harvard DBP1]], [[Engineering:Kitware|Kitware Engineering]] |
| + | __NOTOC__ | ||
| + | = DTI Clustering = | ||
| − | + | In the past, we have demonstrated ways to characterize the strength of connectivity between selected regions in the brain based on several alternative ways to integrate local diffusion tensor measurements into a global field that provided connection strength estimates for distant points. Our current work aims to provide structural description of the white matter as partitioned into coherent fiber bundles and clusters, allowing automatic segmentation of tractography. Furthermore, we are using the segmentation method to enable analysis of diffusion properties along white matter fiber tracts (see the new tract-based morphometry method and the tumor measurement project, below). | |
| + | |||
| + | = Description = | ||
| − | + | ''NA-MIC Software Development'' | |
| − | |||
We are developing tools in the 3D Slicer for automatic clustering of tractographic paths through diffusion tensor MRI (DTI) data. By grouping tractographic paths based on shape and location, the white matter architecture may be more clearly visualized, and interesting properties of the clusters (such as for example FA or Westin's linear measure) may be quantified. | We are developing tools in the 3D Slicer for automatic clustering of tractographic paths through diffusion tensor MRI (DTI) data. By grouping tractographic paths based on shape and location, the white matter architecture may be more clearly visualized, and interesting properties of the clusters (such as for example FA or Westin's linear measure) may be quantified. | ||
| Line 14: | Line 17: | ||
| − | + | ''Clustering Implementation'' | |
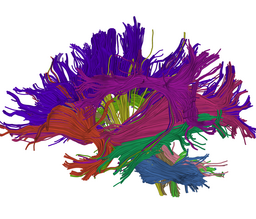
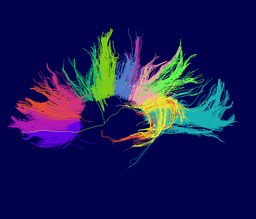
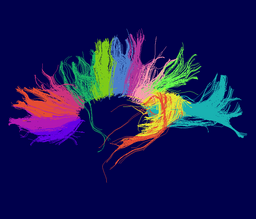
Our implementation uses spectral clustering, a method for grouping data using eigenvectors of a data affinity matrix. This image gives an overview of the method. On the left example input tractographic paths are shown (these were created by manually seeding in the 3D Slicer). The center image shows an embedding of the tracts as points in 2D, where the distance between points is related to their shape similarity. This embedding was calculated as an intermediate step during spectral clustering. The image on the right shows the final output in the 3D Slicer, where tractographic paths are colored by cluster membership. | Our implementation uses spectral clustering, a method for grouping data using eigenvectors of a data affinity matrix. This image gives an overview of the method. On the left example input tractographic paths are shown (these were created by manually seeding in the 3D Slicer). The center image shows an embedding of the tracts as points in 2D, where the distance between points is related to their shape similarity. This embedding was calculated as an intermediate step during spectral clustering. The image on the right shows the final output in the 3D Slicer, where tractographic paths are colored by cluster membership. | ||
| Line 21: | Line 24: | ||
<br clear="all" /> | <br clear="all" /> | ||
| − | + | ''Recent Update: Tract Based Morphometry Method'' | |
| − | Multisubject statistical analyses of DTI in regions of specific white matter tracts have commonly measured only the mean value of a scalar invariant such as the fractional anisotropy (FA). The spatial patterns of FA along fiber tracts have not yet been studied in detail due to the difficulty of finding pointwise correspondences along the lengths of tracts from multiple subjects. We | + | |
| + | Multisubject statistical analyses of DTI in regions of specific white matter tracts have commonly measured only the mean value of a scalar invariant such as the fractional anisotropy (FA). The spatial patterns of FA along fiber tracts have not yet been studied in detail due to the difficulty of finding pointwise correspondences along the lengths of tracts from multiple subjects. We are investigating a new method for calculation of multisubject tract arc length coordinate systems, enabling tract-based morphometry (TBM), the group statistical analysis of tensors or scalar invariants along the length of fiber tracts. | ||
| + | |||
<br clear="all" /> | <br clear="all" /> | ||
[[Image:cingulumAllSubjectsFibers.png|thumb|left|175px|Cingulum bundle with fibers from all 32 subjects (identified using group clustering).]] | [[Image:cingulumAllSubjectsFibers.png|thumb|left|175px|Cingulum bundle with fibers from all 32 subjects (identified using group clustering).]] | ||
| − | |||
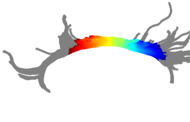
[[Image:cingulum1.png|thumb|left|175px|Arc length coordinates (in color) for one subject.]] | [[Image:cingulum1.png|thumb|left|175px|Arc length coordinates (in color) for one subject.]] | ||
[[Image:cingulum3.png|thumb|left|190px|Arc length coordinates (in color) for another subject.]] | [[Image:cingulum3.png|thumb|left|190px|Arc length coordinates (in color) for another subject.]] | ||
<br clear="all" /> | <br clear="all" /> | ||
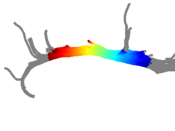
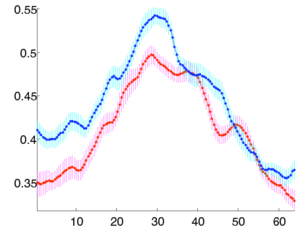
[[Image:cingulumMeanFARightVsLeftAlongTract.png|thumb|left|300px|Mean FA along tract (32 subjects). The left hemisphere FA is shown in blue and the right in red, and anterior is to the left in the plot. Each point represents the mean of subject mean FA values at that arc length coordinate. Bars are standard error across subject means.]] | [[Image:cingulumMeanFARightVsLeftAlongTract.png|thumb|left|300px|Mean FA along tract (32 subjects). The left hemisphere FA is shown in blue and the right in red, and anterior is to the left in the plot. Each point represents the mean of subject mean FA values at that arc length coordinate. Bars are standard error across subject means.]] | ||
| − | [[Image:cingulumPValueOnFiber.png|thumb|left|330px|P-value for left/right hemisphere difference in FA (multiple comparison corrected using permutation testing). Significant differences are found especially in the anterior cingulum bundle.]] | + | [[Image:cingulumPValueOnFiber.png|thumb|left|330px|P-value for left/right hemisphere difference in FA, overlaid on the prototype fiber (multiple comparison corrected using permutation testing). Significant differences are found especially in the anterior cingulum bundle.]] |
<br clear="all" /> | <br clear="all" /> | ||
| − | + | ''Recent Update: Tumor Measurement Project'' | |
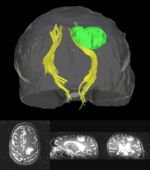
| − | + | [[Image:TumorCSTForWiki.jpg|thumb|right|150px|Tumor and CST clusters displayed in 3D Slicer]] | |
| − | [[Image:TumorCSTForWiki.jpg|thumb|right|150px|Tumor and CST clusters]] | ||
Primary brain tumors lead to changes in the diffusion properties of white matter due to | Primary brain tumors lead to changes in the diffusion properties of white matter due to | ||
edema, infiltration, tract displacement and destruction. Despite investigation of diffusion changes in | edema, infiltration, tract displacement and destruction. Despite investigation of diffusion changes in | ||
| Line 49: | Line 52: | ||
<br clear="all" /> | <br clear="all" /> | ||
| − | + | ''Thesis Results: Automatic Tractography Segmentation'' | |
Atlas creation and automatic labeling has been performed in high-quality DTI datasets from Susumu Mori. Images showing example segmentation results are below. Work is underway to apply this atlas to segment additional datasets to define regions of interest that may be used in the study of schizophrenia. | Atlas creation and automatic labeling has been performed in high-quality DTI datasets from Susumu Mori. Images showing example segmentation results are below. Work is underway to apply this atlas to segment additional datasets to define regions of interest that may be used in the study of schizophrenia. | ||
| − | + | ''Example Results:'' | |
Selected anatomical regions, automatically labeled using the cluster atlas in 3 subjects. | Selected anatomical regions, automatically labeled using the cluster atlas in 3 subjects. | ||
| Line 65: | Line 68: | ||
<br /> | <br /> | ||
| − | + | ''Software'' | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
The software employed in this process includes: | The software employed in this process includes: | ||
| Line 104: | Line 83: | ||
Additional matlab code is used for multiple subject clustering and atlas labeling. | Additional matlab code is used for multiple subject clustering and atlas labeling. | ||
| + | |||
| + | |||
| + | = Key Investigators = | ||
| + | |||
| + | * MIT: Lauren O'Donnell | ||
| + | * Harvard DBP1: Marta Shenton, Monica Lemmond, Alexandra Golby, Carl-Fredrick Westin | ||
| + | * Kitware Engineering: Karthik Krishnan | ||
| + | |||
| + | = Publications = | ||
| + | ''In Print'' | ||
| + | |||
| + | * [http://www.na-mic.org/publications/pages/display?search=Projects%3ADTIClustering&submit=Search&words=all&title=checked&keywords=checked&authors=checked&abstract=checked&sponsors=checked&searchbytag=checked| NA-MIC Publications Database on DTI Fiber Clustering and Fiber-Based Analysis] | ||
| + | |||
| + | ''In Press'' | ||
| + | |||
| + | * Monica E. Lemmond, Lauren J. O'Donnell, Stephen Whalen, and Alexandra J. Golby.Characterizing Diffusion Along White Matter Tracts Affected by Primary Brain Tumors. | ||
| + | Accepted to HBM 2007. | ||
| + | [http://people.csail.mit.edu/lauren/publications/LemmondHBM2007.pdf (pdf)] | ||
| + | |||
| + | [[Category: Segmentation]] [[Category: Slicer]] [[Category:Schizophrenia]] | ||
Latest revision as of 20:20, 11 May 2010
Home < Projects:DTIClusteringBack to NA-MIC Collaborations, MIT Algorithms, Harvard DBP1, Kitware Engineering
DTI Clustering
In the past, we have demonstrated ways to characterize the strength of connectivity between selected regions in the brain based on several alternative ways to integrate local diffusion tensor measurements into a global field that provided connection strength estimates for distant points. Our current work aims to provide structural description of the white matter as partitioned into coherent fiber bundles and clusters, allowing automatic segmentation of tractography. Furthermore, we are using the segmentation method to enable analysis of diffusion properties along white matter fiber tracts (see the new tract-based morphometry method and the tumor measurement project, below).
Description
NA-MIC Software Development
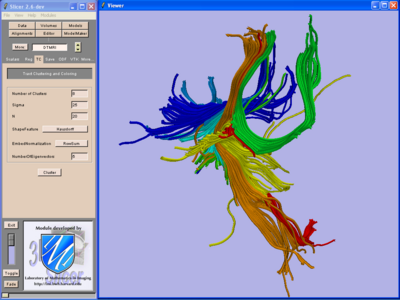
We are developing tools in the 3D Slicer for automatic clustering of tractographic paths through diffusion tensor MRI (DTI) data. By grouping tractographic paths based on shape and location, the white matter architecture may be more clearly visualized, and interesting properties of the clusters (such as for example FA or Westin's linear measure) may be quantified.
Clustering Implementation
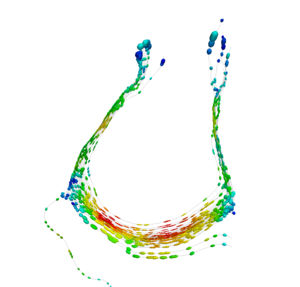
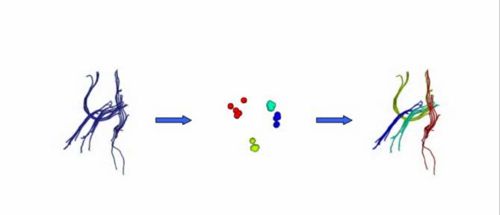
Our implementation uses spectral clustering, a method for grouping data using eigenvectors of a data affinity matrix. This image gives an overview of the method. On the left example input tractographic paths are shown (these were created by manually seeding in the 3D Slicer). The center image shows an embedding of the tracts as points in 2D, where the distance between points is related to their shape similarity. This embedding was calculated as an intermediate step during spectral clustering. The image on the right shows the final output in the 3D Slicer, where tractographic paths are colored by cluster membership.
Recent Update: Tract Based Morphometry Method
Multisubject statistical analyses of DTI in regions of specific white matter tracts have commonly measured only the mean value of a scalar invariant such as the fractional anisotropy (FA). The spatial patterns of FA along fiber tracts have not yet been studied in detail due to the difficulty of finding pointwise correspondences along the lengths of tracts from multiple subjects. We are investigating a new method for calculation of multisubject tract arc length coordinate systems, enabling tract-based morphometry (TBM), the group statistical analysis of tensors or scalar invariants along the length of fiber tracts.
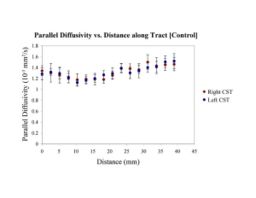
Recent Update: Tumor Measurement Project
Primary brain tumors lead to changes in the diffusion properties of white matter due to edema, infiltration, tract displacement and destruction. Despite investigation of diffusion changes in white matter bordering tumors, these changes have not been quantitatively determined along the length of white matter tracts that may be affected by a tumor. The study of these tracts is especially interesting as the pattern of spread/growth of primary brain tumors is by infiltration along white matter tracts.
Clustered fibers in the region of the corticospinal tract have been used to identify regions of interest for slice-by-slice measurements of this tract's diffusion properties in normals and in tumor subjects. A pilot study (with Monica Lemmond at Harvard Medical School and Stephen Whalen and Alexandra Golby at Brigham and Women's Hospital/HMS) has demonstrated changes in tumor-affected tracts (relative to the contralateral unaffected side) beyond the apparent tumor border. A larger study is currently underway.
Thesis Results: Automatic Tractography Segmentation
Atlas creation and automatic labeling has been performed in high-quality DTI datasets from Susumu Mori. Images showing example segmentation results are below. Work is underway to apply this atlas to segment additional datasets to define regions of interest that may be used in the study of schizophrenia.
Example Results:
Selected anatomical regions, automatically labeled using the cluster atlas in 3 subjects.
Subdivisions of the corpus callosum, labeled using the cluster atlas in 3 subjects.
Software
The software employed in this process includes:
- Slicer DTMRI module VTK classes for tractography.
- Slicer VTK class to compute tract path affinity matrix.
- This matrix contains results of shape comparisons between tract paths.
- Several methods are available: endpoint distance, Hausdorff distance, and mean/covariance distance.
- New ITK class (itkSpectralClustering) clusters data based on an affinity matrix.
- Generally applicable for clustering problems because input is just this matrix.
- New and improved ITK Statistics framework which allows our embedding vectors (such as those in the middle image above) to have variable length and therefore employ more shape information when it is present. Thank you to Karthik Krishnan for reworking the ITK Statistics classes.
All of the code is part of NA-MIC. The VTK classes are in the 3D Slicer DTMRI module, while the ITK class is currently located in the NA-MIC Sandbox and will be included in ITK in the future.
Additional matlab code is used for multiple subject clustering and atlas labeling.
Key Investigators
- MIT: Lauren O'Donnell
- Harvard DBP1: Marta Shenton, Monica Lemmond, Alexandra Golby, Carl-Fredrick Westin
- Kitware Engineering: Karthik Krishnan
Publications
In Print
In Press
- Monica E. Lemmond, Lauren J. O'Donnell, Stephen Whalen, and Alexandra J. Golby.Characterizing Diffusion Along White Matter Tracts Affected by Primary Brain Tumors.
Accepted to HBM 2007. (pdf)