Difference between revisions of "Projects:RegistrationRegularization"
| Line 18: | Line 18: | ||
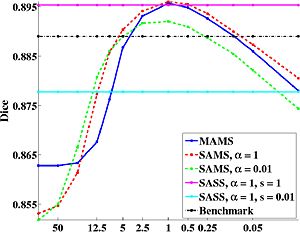
We use dice as the measure of segmentation quality. From the graph below, we note that the optimal parcellation algorithm in all three cases yield a statistically significant improvement over a state-of-the-art benchmark parcellation algorithm [1,2]. The optimal algorithms correspond to a unique balance between atlas “sharpness” and warp regularization. | We use dice as the measure of segmentation quality. From the graph below, we note that the optimal parcellation algorithm in all three cases yield a statistically significant improvement over a state-of-the-art benchmark parcellation algorithm [1,2]. The optimal algorithms correspond to a unique balance between atlas “sharpness” and warp regularization. | ||
| − | [[Image:AvgResults.jpg|thumb|center| | + | [[Image:AvgResults.jpg|thumb|center|300px|Plot of Dice as a function of the warp smoothness S. Note that S is on a log scale. <math>\alpha</math> corresponds to the sharpness of the atlas used.]] |
= Key Investigator = | = Key Investigator = | ||
Revision as of 19:21, 9 November 2007
Home < Projects:RegistrationRegularizationBack to NA-MIC_Collaborations, MIT Algorithms
We propose a unified framework for computing atlases from manually labeled data sets at various degrees of “sharpness” and the joint registration and segmentation of a new brain with these atlases. In non-rigid registration, the tradeoff between warp regularization and image fidelity is typically set empirically. In segmentation, this leads to a probabilistic atlas of arbitrary “sharpness”: weak regularization results in well-aligned training images, producing a “sharp” atlas; strong regularization yields a “blurry” atlas. We study the effects of this tradeoff in the context of cortical surface parcellation, but the framework applies to volume registration as well.
Description
We compare three special cases of our framework, namely:
(1) Progressive registration of a new brain to increasingly “sharp” atlases using increasingly flexible warps, by initializing each registration stage with the optimal warps from a “blurrier” atlas. We call this multiple atlases, multiple warp scales (MAMS).
(2) Progressive registration to a single atlas with increasingly flexible warps. We call this single atlas, multiple warp scales (SAMS).
(3) Registration to a single atlas with fixed constrained warps. We call this single atlas, single warp scale (SASS).
We use dice as the measure of segmentation quality. From the graph below, we note that the optimal parcellation algorithm in all three cases yield a statistically significant improvement over a state-of-the-art benchmark parcellation algorithm [1,2]. The optimal algorithms correspond to a unique balance between atlas “sharpness” and warp regularization.
Key Investigator
MIT: B.T. Thomas Yeo, Mert Sabuncu, Rahul Desikan, Bruce Fischl, Polina Golland
Publication
B.T.T. Yeo, M.R. Sabuncu, R. Desikan, B. Fischl, P. Golland. Effects of Registration Regularization and Atlas Sharpness on Segmentation Accuracy. In Proceedings of MICCAI: International Conference on Medical Image Computing and Computer Assisted Intervention, 683-691, 2007. MICCAI Young Scientist Award.