Difference between revisions of "Projects:LabelSpace"
m |
|||
| Line 16: | Line 16: | ||
techniques for such analysis tend to trade off performance between the two | techniques for such analysis tend to trade off performance between the two | ||
tasks, performing well for one task but developing problems when used for | tasks, performing well for one task but developing problems when used for | ||
| − | the other. | + | the other. We propose label space, a representation that is both flexible |
| − | |||
| − | We propose label space, a representation that is both flexible | ||
and well suited for both tasks. Under this framework, object labels are | and well suited for both tasks. Under this framework, object labels are | ||
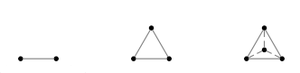
mapped to vertices of a regular simplex, e.g. the unit interval for two | mapped to vertices of a regular simplex, e.g. the unit interval for two | ||
labels, a triangle for three labels, a tetrahedron for four labels, etc. | labels, a triangle for three labels, a tetrahedron for four labels, etc. | ||
This forms a linear space with the property that all labels are equally | This forms a linear space with the property that all labels are equally | ||
| − | spaced. | + | spaced. On examination, this representation has several desirable properties: |
| − | |||
| − | On examination, this representation has several desirable properties: | ||
algebraic operations may be done directly, label uncertainty is expressed as | algebraic operations may be done directly, label uncertainty is expressed as | ||
a weighted mixture of labels, interpolation is unbiased toward any label or | a weighted mixture of labels, interpolation is unbiased toward any label or | ||
| − | the background, and registration may be performed directly. | + | the background, and registration may be performed directly. To demonstrate these properties, we describe variational registration |
| − | |||
| − | To demonstrate these properties, we describe variational registration | ||
directly in this space. Many registration methods fix one of the maps and | directly in this space. Many registration methods fix one of the maps and | ||
align the rest of the set to this fixed map. To remove the bias induced by | align the rest of the set to this fixed map. To remove the bias induced by | ||
Revision as of 17:13, 24 April 2008
Home < Projects:LabelSpaceBack to Georgia Tech Algorithms
Label Space: A Coupled Multi-Shape Representation
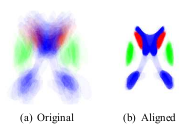
Many techniques for multi-shape representation may often develop inaccuracies stemming from either approximations or inherent variation. Label space is an implicit representation that offers unbiased algebraic manipulation and natural expression of label uncertainty. We demonstrate smoothing and registration on multi-label brain MRI.
Description
Two key aspects of coupled multi-object shape analysis are the choice of representation and subsequent registration to align the sample set. Current techniques for such analysis tend to trade off performance between the two tasks, performing well for one task but developing problems when used for the other. We propose label space, a representation that is both flexible and well suited for both tasks. Under this framework, object labels are mapped to vertices of a regular simplex, e.g. the unit interval for two labels, a triangle for three labels, a tetrahedron for four labels, etc. This forms a linear space with the property that all labels are equally spaced. On examination, this representation has several desirable properties: algebraic operations may be done directly, label uncertainty is expressed as a weighted mixture of labels, interpolation is unbiased toward any label or the background, and registration may be performed directly. To demonstrate these properties, we describe variational registration directly in this space. Many registration methods fix one of the maps and align the rest of the set to this fixed map. To remove the bias induced by arbitrary selection of the fixed map, we align a set of label maps to their intrinsic mean map.
Key Investigators
- Georgia Tech Algorithms: James Malcolm, Yogesh Rathi, Allen Tannenbaum
Publications
J. Malcolm, Y. Rathi, and A. Tannenbaum. "Label Space: A Multi-Object Shape Representation." In Combinatorial Image Analysis, 2008.