Difference between revisions of "Projects:SphericalDemons"
(New page: Back to NA-MIC Collaborations, MIT Algorithms We propose a unified framework for computing atlases from manual...) |
|||
| Line 1: | Line 1: | ||
Back to [[NA-MIC_Internal_Collaborations:StructuralImageAnalysis|NA-MIC Collaborations]], [[Algorithm:MIT|MIT Algorithms]] | Back to [[NA-MIC_Internal_Collaborations:StructuralImageAnalysis|NA-MIC Collaborations]], [[Algorithm:MIT|MIT Algorithms]] | ||
| − | We | + | We present the fast Spherical Demons algorithm for registering two spherical images. By exploiting spherical vector spline |
| + | interpolation theory, we show that a large class of regularizers for the modified demons objective function can be efficiently | ||
| + | implemented on the sphere using convolution. Based on the one parameter subgroups of diffeomorphisms, the resulting registration is | ||
| + | diffeomorphic and fast -- registration of two cortical mesh models with more than 100k nodes takes less than 5 minutes, comparable to the fastest surface registration algorithms. Moreover, the accuracy of our method compares favorably to the popular FreeSurfer | ||
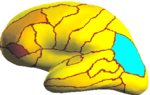
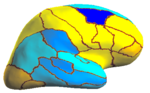
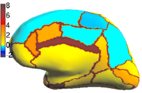
| + | registration algorithm. We validate the technique in two different settings: (1) parcellation in a set of in-vivo cortical surfaces and (2) Brodmann area localization in ex-vivo cortical surfaces. | ||
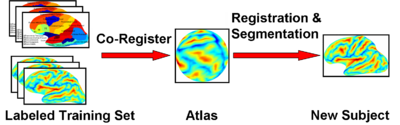
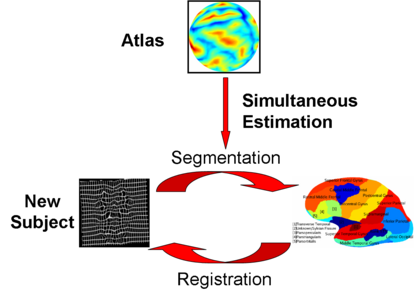
= Description = | = Description = | ||
| − | + | ||
[[Image:RegSeg.png|center|400px|]] | [[Image:RegSeg.png|center|400px|]] | ||
| − | |||
<center> | <center> | ||
| Line 22: | Line 25: | ||
</table> | </table> | ||
</center> | </center> | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
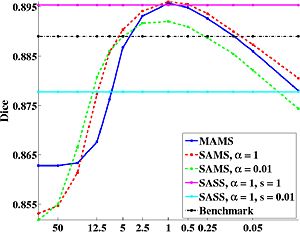
= Experimental Results = | = Experimental Results = | ||
Revision as of 19:59, 9 October 2008
Home < Projects:SphericalDemonsBack to NA-MIC Collaborations, MIT Algorithms
We present the fast Spherical Demons algorithm for registering two spherical images. By exploiting spherical vector spline interpolation theory, we show that a large class of regularizers for the modified demons objective function can be efficiently implemented on the sphere using convolution. Based on the one parameter subgroups of diffeomorphisms, the resulting registration is diffeomorphic and fast -- registration of two cortical mesh models with more than 100k nodes takes less than 5 minutes, comparable to the fastest surface registration algorithms. Moreover, the accuracy of our method compares favorably to the popular FreeSurfer registration algorithm. We validate the technique in two different settings: (1) parcellation in a set of in-vivo cortical surfaces and (2) Brodmann area localization in ex-vivo cortical surfaces.
Description
Experimental Results
We use dice as the measure of segmentation quality. From the graph below, we note that the optimal algorithms correspond to a unique balance between atlas “sharpness” and warp regularization. Our experiments show that the optimal parameter values that correspond to this balance can be determined using cross-validation. The optimal parameter values are robust across subjects, and the same for both co-registration of the training data and registration of a new subject. This suggests that a single atlas at an optimal sharpness is sufficient to achieve the best segmentation results. Furthermore, our experiments also suggest that segmentation accuracy is tolerant up to a small mismatch between atlas sharpness and warp smoothness.
In the figure below, we display the percentage improvement of SASS over FreeSurfer [1,2]. For each of the 35 structures for each hemisphere, we perform a one-sided paired-sampled t-test between SASS and FreeSurfer, where each subject is considered a sample. We use the False Discovery Rate (FDR) to correct for multiple comparisons. In the left hemisphere, SASS achieves statistically significant improvement over FreeSurfer for 17 structures (FDR < 0.05), while the remaining structures yield no statistical difference. In the right hemisphere, SASS achieves improvement for 11 structures (FDR < 0.05), while the remaining structures yield no statistical difference. The p-values for the left and right hemispheres are pooled together for the False Discovery Rate analysis.
[1] Fischl, Sereno and Dale. High-resolution intersubject averaging and a coordinate system for the cortical surface. Human Brain Mapping, 8(4):272--284, 1999
[2] Fischl, van der Kouwe, Destrieux, Halgren, Segonne, Salat, Busa, Seidman, Goldstein, Kennedy, Caviness, Makris, Rosen and Dale. Automatically Parcellating the Human cerebral Cortex. Cerebral Cortex, 14:11--22, 2004
Key Investigators
- MIT Algorithms: [| B.T. Thomas Yeo], Mert Sabuncu, Rahul Desikan, Bruce Fischl, Polina Golland
Publications
In Print
In Press
- B.T.T. Yeo, M.R. Sabuncu, R. Desikan, B. Fischl, P. Golland. "Effects of Registration Regularization and Atlas Sharpness on Segmentation Accuracy". Accepted to Medical Image Analysis, 2008.