Difference between revisions of "Algorithm:Utah"
From NAMIC Wiki
m (Update from Wiki) |
|||
| Line 52: | Line 52: | ||
* Tolga Tasdizen, Suyash Awate, Ross Whitaker and Norman Foster, "MRI Tissue Classification with Neighborhood Statistics: A Nonparametric, Entropy-Minimizing Approach," Proceedings of MICCAI'05, Vol 2, pp. 517-525 | * Tolga Tasdizen, Suyash Awate, Ross Whitaker and Norman Foster, "MRI Tissue Classification with Neighborhood Statistics: A Nonparametric, Entropy-Minimizing Approach," Proceedings of MICCAI'05, Vol 2, pp. 517-525 | ||
| + | |||
| + | = Shape Modeling and Analysis = | ||
| + | |||
| + | == Publications == | ||
| + | * J. Cates, P. Thomas Fletcher, R. Whitaker, M. Styner, M. Shenton. Shape Modeling and Analysis with Entropy-Based Particle Systems. IPMI 2007, accepted. | ||
| + | * J. Cates, P. Thomas Fletcher, R. Whitaker. Entropy-Based Particle Systems for Shape Corresopndence. Mathematical Foundations of Computational Anatomy Workshop, MICCAI 2006. pp. 90-99 Oct 2006. | ||
Revision as of 07:13, 23 March 2007
Home < Algorithm:UtahContents
DTI Processing and Analysis
- Differential Geometry. We will provide methods for computing geodesics and distances between diffusion tensors. Several different metrics will be made available, including a simple linear metric and also a symmetric space (curved) metric. These routines are the building blocks for the routines below.
- Statistics Given a collection of diffusion tensors, compute the average and covariance statistics. This can be done using the metrics and geometry routines above. A general method for testing differences between groups is planned. The hypothesis test also depends on the underlying geometry used.
- Interpolation Interpolation routines will be implemented as a weighted averaging of diffusion tensors in the metric framework. The metric may be chosen so that the interpolation preserves desired properties of the tensors, e.g., orientation, size, etc.
- Filtering We will provide anisotropic filtering of DTI using the full tensor data (as opposed to component-wise filtering). Filtering will also be able to use the different metrics, allowing control over what properties of the tensors are preserved in the smoothing. We have also developed methods for filtering the original diffusion weighted images (DWIs) that takes the Rician distribution of MR noise into account (see MICCAI 2006 paper below).
- Relation to other NA-MIC projects:
- DTI processing: filtering and interpolation are an input to further analysis, such as UNC fiber tract analysis and MGH atlas building.
- DTI statistics: (UNC) will be used in the analysis of tensor data along fiber tracts.
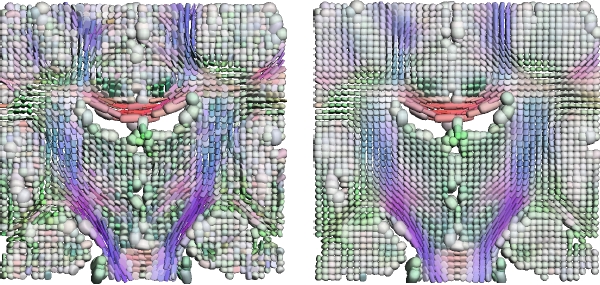
Coronal slice from a noisy diffusion tensor image (left). The same slice after applying our Rician noise DTI filtering method (right).
Publications
- Basu, S., Fletcher, P.T., Whitaker, R., "Rician Noise Removal in Diffusion Tensor MRI," presented at Medical Image Computing and Computer-Assisted Intervention, MICCAI 2006, LNCS 4190, pp. 117--125. PDF of paper
- Corouge, I., Fletcher, P.T., Joshi, S., Gilmore, J.H., and Gerig, G., "Fiber Tract-Oriented Statistics for Quantitative Diffusion Tensor MRI Analysis," Medical Image Analysis 10 (2006), 786--798.
- Corouge, I., Fletcher, P.T., Joshi, S., Gilmore J.H., and Gerig, G., "Fiber Tract-Oriented Statistics for Quantitative Diffusion Tensor MRI Analysis," in Proceedings of Medical Image Computing and Computer-Assisted Intervention (MICCAI 2005), LNCS 3749, pp. 131--138.
Activities
- Developed prototype of DTI geometry package. This includes an abstract class for computing distances and geodesics between tensors, while derived classes can specify the particular metric to use. Current implemented subclasses are the basic linear metric and the symmetric space metric.
- Developed prototype of DTI statistical package. A general class has been developed for computing averages and principal modes of variation of tensor data. The statistics class can use any of the metrics described above.
- We have begun work on a general method for hypothesis testing of differences in two diffusion tensor groups (upcoming IPMI submission). This method works on the full six-dimensional tensor information, rather than derived measures. The hypothesis testing class can also use any of the different tensor metrics.
- Participated in the Programmer's Week (June 2005, Boston). During this week the DTI statistics code was developed and added to the NA-MIC toolkit. See our Progress Report (July 2005). We are also involved in the Statistical Feature Analysis Framework project with Martin Styner (UNC) and Jim Miller (GE).
Software
The diffusion tensor statistics code is now part of the NA-MIC toolkit. To get the code, check out the NA-MIC SandBox (see instructions here) -- our code is in the "DiffusionTensorStatistics" directory.
MRI Segmentation
- We have implemented the MRI Tissue Classification Algorithm described in [1]. Classes for non-parametric density estimation and automatic parameter selection have been implemented as the basic framework on which we build the classification algorithm.
- The stochastic non-parametric density estimation framework is very general and allows the user to change kernel types (we have coded isotropic Gaussian, but additional kernels can easily be derived from the same parent class) and sampler types (for example local vs. global image sampling as well as sampling in non-image data) as template parameters.
- The classification class uses the stochastic non-parametric density estimation framework to implement the algorithm in [1].
- An existing ITK bias correction method has been incorporated into the method.
- Currently, we are registering atlas images to our data using the stand-alone LandmarkInitializedMutualInformationRegistration application. Ideally, we'd like to incorporate an exiting registration algorithm into our code so that classification can be carried out in one step. The initialization to the registration can be provided as command line arguments.
Publications
- Tolga Tasdizen, Suyash Awate, Ross Whitaker and Norman Foster, "MRI Tissue Classification with Neighborhood Statistics: A Nonparametric, Entropy-Minimizing Approach," Proceedings of MICCAI'05, Vol 2, pp. 517-525
Shape Modeling and Analysis
Publications
- J. Cates, P. Thomas Fletcher, R. Whitaker, M. Styner, M. Shenton. Shape Modeling and Analysis with Entropy-Based Particle Systems. IPMI 2007, accepted.
- J. Cates, P. Thomas Fletcher, R. Whitaker. Entropy-Based Particle Systems for Shape Corresopndence. Mathematical Foundations of Computational Anatomy Workshop, MICCAI 2006. pp. 90-99 Oct 2006.