Projects:ConformalFlatteningRegistration

Back to NA-MIC_Collaborations, Georgia Tech Algorithms

Conformal Flattening Registration

The goal of this project is for better visualizing and computation of neural activity from fMRI brain imagery. Also, with this technique, shapes can be mapped to spheres for shape analysis, registration or other purposes. Our technique is based on conformal mappings which map genus-zero surface: in fMRI case cortical or other surfaces, onto a sphere in an angle preserving manner.

The explicit transform is obtained by solving a partial differential equation. Such transform will map the original surface to a plane(flattening) and then one can use classic stereographic transformation to map the plane to a sphere.

Description

The process of the algorithm is briefly given below:

1. The conformal mapping f is defined on the originla surface Σ as [math]\triangle f = (\frac{\partial}{\partial u} - i\frac{\partial}{\partial v})\delta_p[/math]. In that u and v are the conformal coordinates defined on the surface and the δ_p is a Dirac function whose value is non-zero only at point p. By solving this partial differential equation the mapping f can be obtained.
2. To solve that equation on the discrete mesh representation of the surface, finite element method(FEM) is used. The problem is turned to solving a linear system D'x = b. Since b is complex vector, the real and imaginary parts of the mapping f can be calculated separately by two linear system.
3. Having the mapping f, the original surface can be mapped to a plane.
4. Further, the plane can be mapped to a sphere by the stereographic projection.

Also, in the work of Multiscale Shape Segmentation, conformal flattening is used as the first step for remeshing the surface.

Progress

This algorithm is now written into SandBox as itkConformalFlatteningFilter. More test is being made and then hopefully can be integrated into the ITK CVS repository.

===>

===>

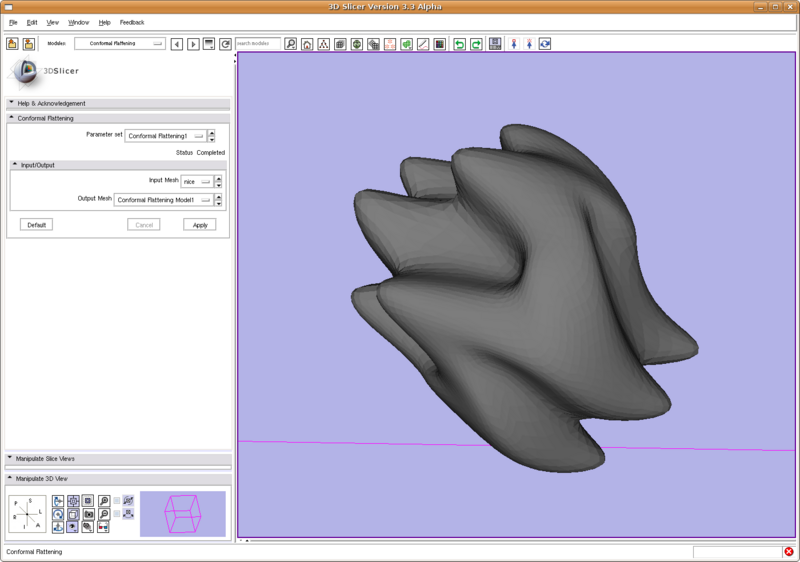
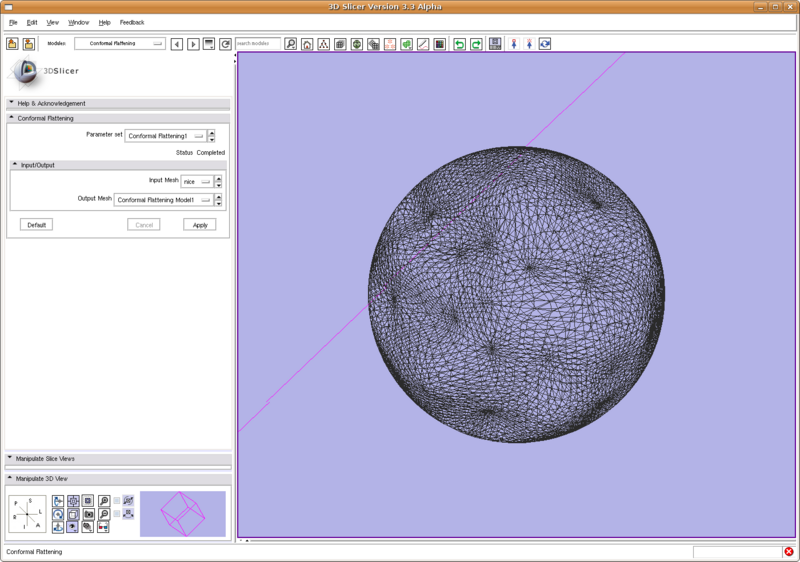
Conformal Flattening Slicer3 module

The conformal flattening algorithm has been put into ITK in the Insight Journal 2006. During the project week 2008, it is further put into Slicer3 as a command line module. Below we show two screen shots of using it.

Acceleration

The major computation happens in the solution of the linear system using conjugate gradient method. This can be accelerated using the pre-conditioning technique.

Key Investigators

• Georgia Tech Algorithms: Yi Gao, John Melonakos, Allen Tannenbaum

Publications

• Y. Gao, J. Melonakos, and A. Tannenbaum. Conformal Flattening ITK Filter. MICCAI 2006 Open Source Workshop / Insight Journal, 2006 NA-MIC Publications Database