Difference between revisions of "Algorithm:GATech:Finsler Active Contour DWI"
m (Update from Wiki) |
|||
| Line 3: | Line 3: | ||
'''Objective:''' | '''Objective:''' | ||
| − | We want to extract the white matter tracts from Diffusion | + | We want to extract the white matter tracts from Diffusion Weighted MRI scans. The idea is to use directional information in a new anisotropic energy functional based on Finsler geometry. |
'''Progress:''' | '''Progress:''' | ||
| − | We have implemented the algorithm in | + | We have implemented the algorithm in Matlab/C using the Fast Sweeping algorithm. We are in the process of porting the code to ITK. |
| − | We are continuing to work on our new framework for white matter tractography in high angular resolution diffusion data. We base our work on concepts from Finsler geometry. Namely, a direction-dependent local cost is defined based on the diffusion data for every direction on the unit sphere. Minimum cost curves are determined by solving the Hamilton-Jacobi-Bellman using the | + | We are continuing to work on our new framework for white matter tractography in high angular resolution diffusion data. We base our work on concepts from Finsler geometry. Namely, a direction-dependent local cost is defined based on the diffusion data for every direction on the unit sphere. Minimum cost curves are determined by solving the Hamilton-Jacobi-Bellman using the Fast Sweeping algorithm. Classical costs based on the diffusion tensor field can be seen as a special case. While the minimum cost (or equivalently the travel time of a particle moving along the curve) and the anisotropic front propagation frameworks are related, front speed is related to particle speed through a Legendre transformation which can severely impact anisotropy information for front propagation techniques. Implementation details and results on high angular diffusion data show that this method can successfully take advantage of the increased angular resolution in high b-value diffusion weighted data despite lower signal to noise ratio. (See Figures 1 and 2 at the end of this page for examples. This method also works nicely for the segmentation of blood vessels as is indicated in Figure 3.) |
| − | + | ''Data'' | |
| − | + | We are using Harvard's high angular resolution datasets which currently consist of a population of 12 schizophrenics and 12 normal controls. | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | * Working 3D implementation in Matlab using the C-based | + | ''Results'' |
| − | * Currently porting to ITK. | + | |
| + | *[[Image:Case24-coronal-tensors-edit.png | 600px]] Detailed View of the Cingulum Bundle Anchor Tract | ||
| + | *[[Image:Case25-sagstream-tensors-edit.png | 600px]] Streamline Comparison | ||
| + | *[[Image:Case26-anterior.png | 400px]] Anterior View of the Cingulum Bundle Anchor Tract | ||
| + | *[[Image:Case26-posterior.png | 400px]] Posterior View of the Cingulum Bundle Anchor Tract | ||
| + | *[[Image:Tracts1.png | 400px]] Fiber tracking from high resolution data set. | ||
| + | *[[Image:Tracts2.png | 400px]] Comparison of technique with streamline based on tensor field. | ||
| + | *[[Image:Vessels1.png | 400px]] Vessel Segmentation. | ||
| + | |||
| + | ''Project Status'' | ||
| + | *Working 3D implementation in Matlab using the C-based Mex functions. | ||
| + | *Currently porting to ITK. | ||
''References:'' | ''References:'' | ||
| − | * | + | * J. Melonakos, V. Mohan, M. Niethammer, K. Smith, M. Kubicki, and A. Tannenbaum. Under review. |
| − | + | * J. Melonakos, E. Pichon, S. Angenet, and A. Tannenbaum. Finsler Active Contours for Directional Segmentation. Submitted to IEEE Transactions on Pattern Analysis and Machine Intelligence. | |
* E. Pichon and A. Tannenbaum. Curve segmentation using directional information, relation to pattern detection. In IEEE International Conference on Image Processing (ICIP), volume 2, pages 794-797, 2005. | * E. Pichon and A. Tannenbaum. Curve segmentation using directional information, relation to pattern detection. In IEEE International Conference on Image Processing (ICIP), volume 2, pages 794-797, 2005. | ||
| − | |||
* E. Pichon, C-F Westin, and A. Tannenbaum. A Hamilton-Jacobi-Bellman approach to high angular resolution diffusion tractography. In International Conference on Medical Image Computing and Computer Assisted Intervention (MICCAI), pages 180-187, 2005 | * E. Pichon, C-F Westin, and A. Tannenbaum. A Hamilton-Jacobi-Bellman approach to high angular resolution diffusion tractography. In International Conference on Medical Image Computing and Computer Assisted Intervention (MICCAI), pages 180-187, 2005 | ||
'''Key Investigators:''' | '''Key Investigators:''' | ||
| − | * Georgia Tech: John Melonakos, | + | * Georgia Tech: John Melonakos, Vandana Mohan, Allen Tannenbaum |
| − | * Harvard/BWH: C-F Westin, Martha Shenton | + | * Harvard/BWH: Marek Kubicki, Marc Niethammer, Kate Smith, C-F Westin, Martha Shenton |
'''Links:''' | '''Links:''' | ||
Revision as of 13:53, 2 April 2007
Home < Algorithm:GATech:Finsler Active Contour DWIBack to NA-MIC_Collaborations
Objective:
We want to extract the white matter tracts from Diffusion Weighted MRI scans. The idea is to use directional information in a new anisotropic energy functional based on Finsler geometry.
Progress:
We have implemented the algorithm in Matlab/C using the Fast Sweeping algorithm. We are in the process of porting the code to ITK.
We are continuing to work on our new framework for white matter tractography in high angular resolution diffusion data. We base our work on concepts from Finsler geometry. Namely, a direction-dependent local cost is defined based on the diffusion data for every direction on the unit sphere. Minimum cost curves are determined by solving the Hamilton-Jacobi-Bellman using the Fast Sweeping algorithm. Classical costs based on the diffusion tensor field can be seen as a special case. While the minimum cost (or equivalently the travel time of a particle moving along the curve) and the anisotropic front propagation frameworks are related, front speed is related to particle speed through a Legendre transformation which can severely impact anisotropy information for front propagation techniques. Implementation details and results on high angular diffusion data show that this method can successfully take advantage of the increased angular resolution in high b-value diffusion weighted data despite lower signal to noise ratio. (See Figures 1 and 2 at the end of this page for examples. This method also works nicely for the segmentation of blood vessels as is indicated in Figure 3.)
Data
We are using Harvard's high angular resolution datasets which currently consist of a population of 12 schizophrenics and 12 normal controls.
Results
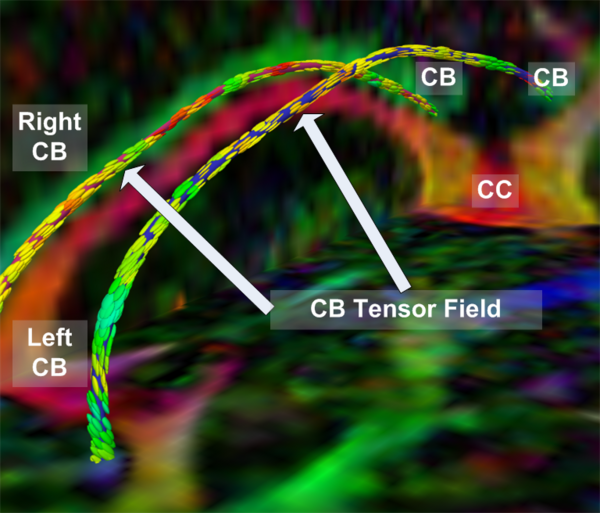 Detailed View of the Cingulum Bundle Anchor Tract
Detailed View of the Cingulum Bundle Anchor Tract Streamline Comparison
Streamline Comparison Anterior View of the Cingulum Bundle Anchor Tract
Anterior View of the Cingulum Bundle Anchor Tract Posterior View of the Cingulum Bundle Anchor Tract
Posterior View of the Cingulum Bundle Anchor Tract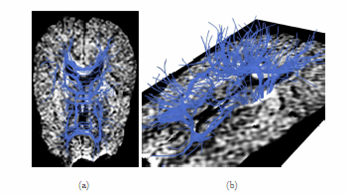 Fiber tracking from high resolution data set.
Fiber tracking from high resolution data set.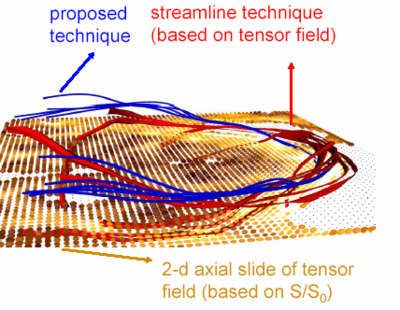 Comparison of technique with streamline based on tensor field.
Comparison of technique with streamline based on tensor field.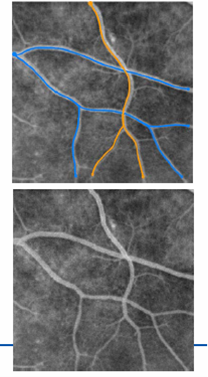 Vessel Segmentation.
Vessel Segmentation.
Project Status
- Working 3D implementation in Matlab using the C-based Mex functions.
- Currently porting to ITK.
References:
- J. Melonakos, V. Mohan, M. Niethammer, K. Smith, M. Kubicki, and A. Tannenbaum. Under review.
- J. Melonakos, E. Pichon, S. Angenet, and A. Tannenbaum. Finsler Active Contours for Directional Segmentation. Submitted to IEEE Transactions on Pattern Analysis and Machine Intelligence.
- E. Pichon and A. Tannenbaum. Curve segmentation using directional information, relation to pattern detection. In IEEE International Conference on Image Processing (ICIP), volume 2, pages 794-797, 2005.
- E. Pichon, C-F Westin, and A. Tannenbaum. A Hamilton-Jacobi-Bellman approach to high angular resolution diffusion tractography. In International Conference on Medical Image Computing and Computer Assisted Intervention (MICCAI), pages 180-187, 2005
Key Investigators:
- Georgia Tech: John Melonakos, Vandana Mohan, Allen Tannenbaum
- Harvard/BWH: Marek Kubicki, Marc Niethammer, Kate Smith, C-F Westin, Martha Shenton
Links: