Difference between revisions of "2012 Summer Project Week:RidgeExtractionAtrialWallSegmentation"
| Line 47: | Line 47: | ||
<h3>Progress</h3> | <h3>Progress</h3> | ||
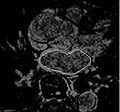
We have developed topological simplification methods for removing noisy local maxima. The resulting ridge detection algorithm shows average error less then 2 pixels compared to the manual segmentation. | We have developed topological simplification methods for removing noisy local maxima. The resulting ridge detection algorithm shows average error less then 2 pixels compared to the manual segmentation. | ||
| + | |||
| + | This week: | ||
| + | * We have developed general error computation framework for segmentation features quantitative comparison. | ||
| + | * Two topological simplification algorithms were implemented and compared to a regular edge base segmentation. Both implemented algorithms show about 40% reduction in error. | ||
| + | * In the future, we plan to compare more topological simplifications to improve the error. | ||
| + | |||
</div> | </div> | ||
</div> | </div> | ||
| − | |||
| − | |||
==References== | ==References== | ||
# Edelsbrunner, H., Harer, J., & Zomorodian, A. (2003). Hierarchical Morse--Smale Complexes for Piecewise Linear 2-Manifolds. Discrete and Computational Geometry, 30(1), 87-107. doi:10.1007/s00454-003-2926-5 | # Edelsbrunner, H., Harer, J., & Zomorodian, A. (2003). Hierarchical Morse--Smale Complexes for Piecewise Linear 2-Manifolds. Discrete and Computational Geometry, 30(1), 87-107. doi:10.1007/s00454-003-2926-5 | ||
# Szymczak, A., Stillman, A., Tannenbaum, A., & Mischaikow, K. (2006). Coronary vessel trees from 3D imagery: a topological approach. Medical image analysis, 10(4), 548-59. doi:10.1016/j.media.2006.05.002 | # Szymczak, A., Stillman, A., Tannenbaum, A., & Mischaikow, K. (2006). Coronary vessel trees from 3D imagery: a topological approach. Medical image analysis, 10(4), 548-59. doi:10.1016/j.media.2006.05.002 | ||
Latest revision as of 13:01, 22 June 2012
Home < 2012 Summer Project Week:RidgeExtractionAtrialWallSegmentationBackground
Catheter ablation has been proposed for treatment of atrial fibrillation arrhythmia. MRI data is used to explore lesion ablation and scarification locations are extracted from MRI image data. In addition, MRI analysis may help to predict if the ablation procedure will help a patient or not. Many of these image analysis tasks are largely based on segmentation of left atrial wall, which is done manually or semi-automatically. Automatic segmentation uses moving contours or surfaces (interfaces) to segment image data by minimizing a predefined energy function. These moving interfaces are highly affected by image data, which can be thought as a force field pushing the interface to features of choice. Thus, the choice of interface attracting image features is critical.
Key Investigators
- BU: Arie Nakhmani
- BU and CCC UAB: Allen Tannenbaum
Objective
We are exploring different image features which are appropriate for an automatic segmentation. Our objective is to compare different topological extrema ranking algorithms (including maximum persistence [1,2] and perceptual ridge importance) to provide the most appropriate features, based on expert's manual segmentation.
Approach, Plan
- Implementing the comparison framework
- Ellipsoidal MRI transform
- Local ridge extraction
- Topological persistence algorithm implementation
- Comparison of different topological simplification approaches
Progress
We have developed topological simplification methods for removing noisy local maxima. The resulting ridge detection algorithm shows average error less then 2 pixels compared to the manual segmentation.
This week:
- We have developed general error computation framework for segmentation features quantitative comparison.
- Two topological simplification algorithms were implemented and compared to a regular edge base segmentation. Both implemented algorithms show about 40% reduction in error.
- In the future, we plan to compare more topological simplifications to improve the error.
References
- Edelsbrunner, H., Harer, J., & Zomorodian, A. (2003). Hierarchical Morse--Smale Complexes for Piecewise Linear 2-Manifolds. Discrete and Computational Geometry, 30(1), 87-107. doi:10.1007/s00454-003-2926-5
- Szymczak, A., Stillman, A., Tannenbaum, A., & Mischaikow, K. (2006). Coronary vessel trees from 3D imagery: a topological approach. Medical image analysis, 10(4), 548-59. doi:10.1016/j.media.2006.05.002