Difference between revisions of "Projects:NonparametricSegmentation"
| Line 54: | Line 54: | ||
In a third experiment, we evaluated the spectral label fusion. We automatically segment the left atrium of the heart in a set of 16 electro-cardiogram gated (0.2 mmol/kg) Gadolinium- DTPA contrast-enhanced cardiac MRA images (CIDA sequence, TR=4.3ms, TE=2.0ms, θ = 40º, in-plane resolution varying from 0.51mm to 0.68mm, slice thickness varying from 1.2mm to 1.7mm, 512 × 512 × 96, -80 kHz bandwidth, atrial diastolic ECG timing to counteract considerable volume changes of the left atrium). The left atrium was manually segmented in each image by an expert. We set the UCM threshold (see scheme) to ρ = 0.2 for the 2D and ρ = 0 for the 3D watershed. We perform leave-one-out experiments by treating one subject as the test image and the remaining 15 subjects as the training set. We use the Dice score and the modified (average) Hausdorff distance between the automatic and expert segmentations as quantitative measures of segmentation quality. We compare our method to majority voting (MV) and intensity-weighted label fusion (IW). | In a third experiment, we evaluated the spectral label fusion. We automatically segment the left atrium of the heart in a set of 16 electro-cardiogram gated (0.2 mmol/kg) Gadolinium- DTPA contrast-enhanced cardiac MRA images (CIDA sequence, TR=4.3ms, TE=2.0ms, θ = 40º, in-plane resolution varying from 0.51mm to 0.68mm, slice thickness varying from 1.2mm to 1.7mm, 512 × 512 × 96, -80 kHz bandwidth, atrial diastolic ECG timing to counteract considerable volume changes of the left atrium). The left atrium was manually segmented in each image by an expert. We set the UCM threshold (see scheme) to ρ = 0.2 for the 2D and ρ = 0 for the 3D watershed. We perform leave-one-out experiments by treating one subject as the test image and the remaining 15 subjects as the training set. We use the Dice score and the modified (average) Hausdorff distance between the automatic and expert segmentations as quantitative measures of segmentation quality. We compare our method to majority voting (MV) and intensity-weighted label fusion (IW). | ||
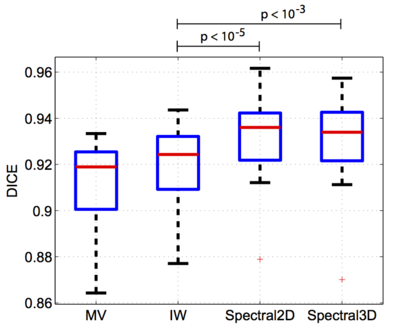
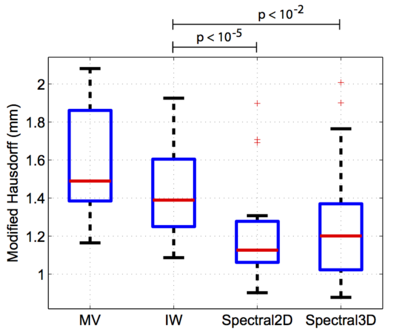
| − | In the figures below, we present dice volume overlap and modified Hausdorff distance for each algorithm. The improvements in segmentation accuracy between the proposed method and IW are statistically significant (p<10−5). | + | In the figures below, we present dice volume overlap (left) and modified Hausdorff distance (right) for each algorithm. The improvements in segmentation accuracy between the proposed method and IW are statistically significant (p<10−5). |
[[File:boxplotDice.png|400px]] [[File:boxplotHausdorff.png|400px]] | [[File:boxplotDice.png|400px]] [[File:boxplotHausdorff.png|400px]] | ||
Revision as of 20:12, 28 November 2012
Home < Projects:NonparametricSegmentationBack to NA-MIC Collaborations, MIT Algorithms,
Nonparametric Segmentation
We propose a non-parametric, probabilistic model for the automatic segmentation of medical images, given a training set of images and corresponding label maps. The resulting inference algorithms we develop rely on pairwise registrations between the test image and individual training images. The training labels are then transferred to the test image and fused to compute a final segmentation of the test subject. Label fusion methods have been shown to yield accurate segmentation, since the use of multiple registrations captures greater inter-subject anatomical variability and improves robustness against occasional registration failures, cf. [1,2,3]. To the best of our knowledge, this project investigates the first comprehensive probabilistic framework that rigorously motivates label fusion as a segmentation approach. The proposed framework allows us to compare different label fusion algorithms theoretically and practically. In particular, recent label fusion or multi-atlas segmentation algorithms are interpreted as special cases of our framework.
Next to the non-parametric model, we presented a new technique that exploits boundary information in the intensity image, referred to as "Spectral Label Fusion". Contour and texture cues are extracted from the image and combined with the label map in a spectral clustering framework. This approach offers advantages for datasets with high variability, making the segmentation less prone to registration errors. We achieve the integration by letting the weights of the graph Laplacian depend on image data, as well as atlas-based label priors. The extracted contours are converted to regions, arranged in a hierarchy depending on the strength of the separating boundary. Finally, we construct the segmentation by a region-wise, instead of voxel-wise voting. To derive the region-based voting, we modify the previous non-parametric, probabilistic model.
Description
Probabilistic Model
We instantiate our model in the context of brain MRI segmentation, where whole brain MRI volumes are automatically parcellated into the following anatomical Regions of Interest (ROI): white matter (WM), cerebral cortex(CT), lateral ventricle (LV), hippocampus(HP), amygdala (AM), thalamus (TH), caudate (CA), putamen (PU), palladum (PA). The proposed non-parametric model yields four types of label fusion algorithms:
(1) Majority Voting: The algorithm computes the most frequent propagated labels at each voxel independently. This is a segmentation algorithm commonly used in practice, e.g. [2,3].
(2) Local Label Fusion: An independent weighted averaging of propagated labels, where the weights vary at each voxel and are a function of the intensity difference between the training image and test image.
(3) Semi-Local Label Fusion: Propagated labels are fused in a weighted fashion using a variational mean field algorithm. The weights are encouraged to be similar in local patches.
(4) Global Label Fusion: Propagated labels are fused in a weighted fashion using an Expectation Maximization algorithm. The weights are global, i.e., there is a single weight for each training subject.
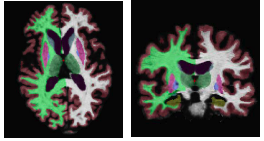
The following figure shows an example segmentation obtained via Local Label Fusion.
Spectral Label Fusion
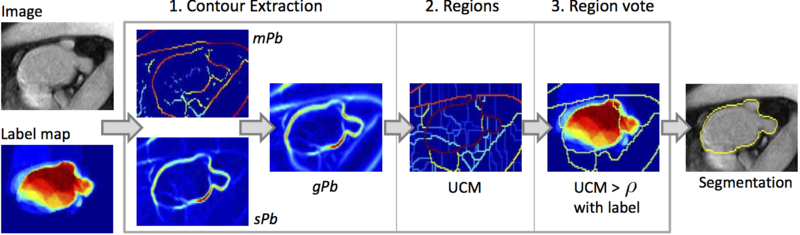
Spectral label fusion consists of three steps, as illustrated in the figure below. The input to the algorithm are the new image to be segmented and the probabilistic label map.
(1): The first step extracts the boundaries from the image and label map, joins them in the spectral framework, and produces weighted contours. The boundary extraction we employ concepts based on spectral clustering, as presented in~[5].
(2): In the second step, the extracted contours give rise to regions, partitioning the image. We obtain the parcellation of the image with the watershed algorithm.
(3): In the third step, we assign a label to each region based on the input label map, producing the final segmentation. For the region-based voting, we replace the assumption of independent voxel samples from the probabilistic framework with the Markov property. Crucial is the selection of image-specific neighborhoods that capture the relevant information, as done in the second step.
Experiments
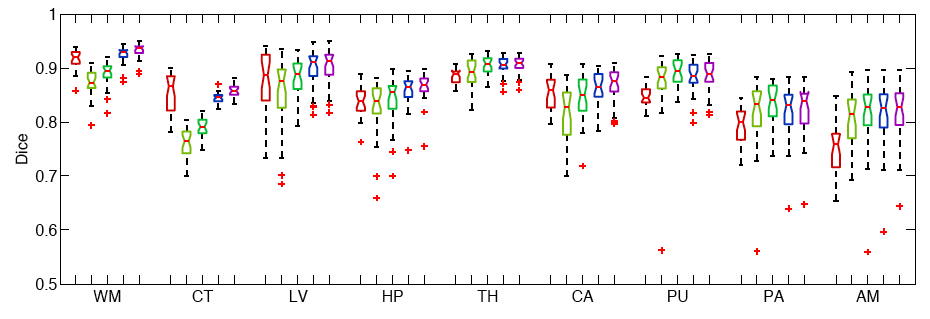
We conduct two sets of experiments to validate our framework. In the first set of experiments, we use 39 brain MRI scans – with manually segmented white matter, cerebral cortex, ventricles and subcortical structures – to compare different label fusion algorithms and the widely-used Freesurfer whole-brain segmentation tool [4].
The following figure shows the Boxplots of Dice scores for all methods: Freesurfer (red), Majority Voting (yellow), Global Weighted Fusion (green), Local Weighted Voting (blue), Semi-local Weighted Fusion (purple).
Our results indicate that the proposed framework yields more accurate segmentation than Freesurfer and Majority Voting.
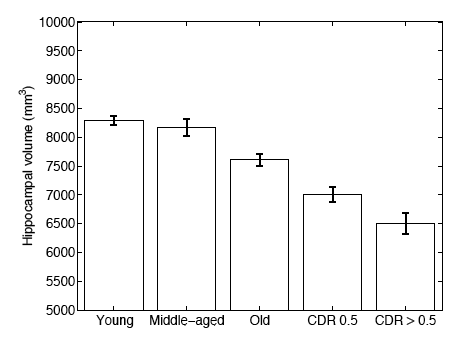
In a second experiment, we use brain MRI scans of 304 subjects to demonstrate that the proposed segmentation tool is sufficiently sensitive to robustly detect hippocampal atrophy that foreshadows the onset of Alzheimer’s Disease. The following figure plots the Average Hippocampal volumes for five different groups (young: younger than 30, middle aged: older than 30, younger than 60; old: older than 60; patients with MCI, and AD patients) in the 304 subjects of Experiment 2. Error bars indicate standard error.
In a third experiment, we evaluated the spectral label fusion. We automatically segment the left atrium of the heart in a set of 16 electro-cardiogram gated (0.2 mmol/kg) Gadolinium- DTPA contrast-enhanced cardiac MRA images (CIDA sequence, TR=4.3ms, TE=2.0ms, θ = 40º, in-plane resolution varying from 0.51mm to 0.68mm, slice thickness varying from 1.2mm to 1.7mm, 512 × 512 × 96, -80 kHz bandwidth, atrial diastolic ECG timing to counteract considerable volume changes of the left atrium). The left atrium was manually segmented in each image by an expert. We set the UCM threshold (see scheme) to ρ = 0.2 for the 2D and ρ = 0 for the 3D watershed. We perform leave-one-out experiments by treating one subject as the test image and the remaining 15 subjects as the training set. We use the Dice score and the modified (average) Hausdorff distance between the automatic and expert segmentations as quantitative measures of segmentation quality. We compare our method to majority voting (MV) and intensity-weighted label fusion (IW). In the figures below, we present dice volume overlap (left) and modified Hausdorff distance (right) for each algorithm. The improvements in segmentation accuracy between the proposed method and IW are statistically significant (p<10−5).
Conclusion
In this work, we investigate a generative model that leads to label fusion style image segmentation methods. Within the proposed framework, we derived various algorithms that combine transferred training labels into a single segmentation estimate. With a dataset of 39 brain MRI scans and corresponding label maps obtained from an expert, we experimentally compared these segmentation algorithms with Freesurfer’s widely-used atlas-based segmentation tool [4]. Our results suggested that the proposed framework yields accurate and robust segmentation tools that can be employed on large multi-subject datasets. In a second experiment, we employed one of the developed segmentation algorithms to compute hippocampal volumes in MRI scans of 304 subjects. A comparison of these measurements across clinical and age groups indicate that the proposed algorithms are sufficiently sensitive to detect hippocampal atrophy that precedes probable onset of Alzheimer’s Disease.
Literature
[1] X. Artaechevarria, A. Munoz-Barrutia, and C. Ortiz de Solorzano. Combination strategies in multi-atlas image segmentation: Application to brain MR data. IEEE Tran. Med. Imaging, 28(8):1266 – 1277, 2009.
[2] R.A. Heckemann, J.V. Hajnal, P. Aljabar, D. Rueckert, and A. Hammers. Automatic anatomical brain MRI segmentation combining label propagation and decision fusion. Neuroimage, 33(1):115–126, 2006.
[3] T. Rohlfing, R. Brandt, R. Menzel, and C.R. Maurer. Evaluation of atlas selection strategies for atlas-based image segmentation with application to confocal microscopy images of bee brains. NeuroImage, 21(4):1428–1442, 2004.
[4] Freesurfer Wiki. http://surfer.nmr.mgh.harvard.edu.
[5] Arbelaez, P., Maire, M., Fowlkes, C., Malik, J.: Contour detection and hierarchical image segmentation. IEEE Trans. on Pat. Anal. Mach. Intel. 33(5), 898–916 (2011)
Key Investigators
- MIT: Mert R. Sabuncu, B.T. Thomas Yeo, Koen Van Leemput, Michal Depa and Polina Golland
- Harvard: Koen Van Leemput and Bruce Fischl
Publications
NA-MIC Publications Database on Nonparametric Models for Supervised Image Segmentation