Difference between revisions of "Projects:KPCA LLE KLLE ShapeAnalysis"
| Line 1: | Line 1: | ||
| + | == Objective == | ||
| + | To compare various shape representation techniques like linear PCA (LPCA), kernel PCA (KPCA), locally linear embedding (LLE) and | ||
| + | kernel locally linear embedding (KLLE). | ||
| + | |||
| + | == Overview == | ||
| + | |||
| + | === Shape Representation === | ||
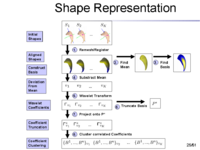
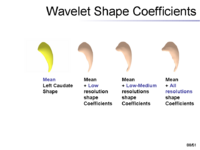
| + | The surfaces are represented as the zero level set of a signed distance function and shape learning is performed on the embeddings of these shapes. We carry out some experiments to see how well each of these methods can represent a shape, given the training set. We tested the performance of these methods on shapes of left caudate nucleus and left hippocampus. The training set of left caudate nucleus consisted of 26 data sets and the test set contained 3 volumes. Error between a particular shape representation and | ||
| + | ground truth was calculated by computing the number of mislabeled voxels using each of the methods. Figure 1 gives the error | ||
| + | using each of the methods. Similar tests were done on a training set of 20 hippocampus data with 3 test volumes. Figure 2 gives the error table for each of the methods [1]. | ||
| + | |||
| + | [[Image:Gatech_SW_representation.png|thumb|200px|Figure 1: Steps of the Shape Representation using Spherical Wavelets]] | ||
| + | [[Image:Gatech_SW_mscale_shape.png|thumb|200px|Figure 2: A shape is represented using spherical wavelet coefficients]] | ||
| + | |||
| + | === Segmentation === | ||
| + | Based on this representation, we derive a parametric active surface evolution using the multiscale prior coefficients as parameters for our optimization procedure to naturally include the prior for segmentation. Additionally, the optimization method can be applied in a coarse-to-fine manner. | ||
| + | |||
| + | === Results === | ||
| + | We applied our algorithm to the caudate nucleus, a brain structure of interest in the study of schizophrenia [2]. Our validation shows our algorithm is computationally efficient and outperforms the Active Shape Model (ASM) algorithm, by capturing finer shape details. | ||
| + | |||
| + | == References == | ||
| + | * [1] Nain D, Haker S, Bobick A, Tannenbaum A. Multiscale 3D Shape Analysis using Spherical Wavelets. Proc MICCAI, Oct 26-29 2005; p 459-467 [1] | ||
| + | * [2] Nain D, Haker S, Bobick A, Tannenbaum A. Shape-driven 3D Segmentation using Spherical Wavelets. Proc MICCAI, Oct 2-5, 2006. PDF of paper | ||
| + | |||
| + | == Key Investigators == | ||
| + | * Core 1: | ||
| + | ** Georgia Tech: Delphine Nain, Aaron Bobick, Allen Tannenbaum | ||
| + | ** Harvard SPL: Steven Haker | ||
| + | |||
| + | == Collaborators == | ||
| + | |||
| + | * Core 1: Martin Styner (UNC) | ||
| + | * Core 2: Jim Miller (GE), Luis Ibanez (Kitware) | ||
| + | * Core 3: James Levitt, Marc Niethammer, Sylvain Bouix, Martha Shenton (Harvard PNL) | ||
| + | |||
| + | == Links: == | ||
| + | * Paper presented in [[MICCAI_2006|MICCAI 2006, Copenhagen, October 2 - 4, 2006 ]] | ||
| + | * Code: [[NA-MIC/Projects/Structural/Shape_Analysis/Spherical_Wavelets_in_ITK|ITK Spherical Wavelet Transform Filter]] | ||
| + | * [[Algorithm:GATech|Georgia Tech Summary Page]] | ||
| + | * [[NA-MIC_Collaborations|NA-MIC_Collaborations]] | ||
| + | |||
| + | |||
| + | |||
Y. Rathi, S. Dambreville, and A. Tannenbaum. "Comparative Analysis of Kernel Methods for Statistical Shape Learning", In CVAMIA held in conjunction with ECCV, 2006. | Y. Rathi, S. Dambreville, and A. Tannenbaum. "Comparative Analysis of Kernel Methods for Statistical Shape Learning", In CVAMIA held in conjunction with ECCV, 2006. | ||
Revision as of 15:05, 2 April 2007
Home < Projects:KPCA LLE KLLE ShapeAnalysisContents
Objective
To compare various shape representation techniques like linear PCA (LPCA), kernel PCA (KPCA), locally linear embedding (LLE) and kernel locally linear embedding (KLLE).
Overview
Shape Representation
The surfaces are represented as the zero level set of a signed distance function and shape learning is performed on the embeddings of these shapes. We carry out some experiments to see how well each of these methods can represent a shape, given the training set. We tested the performance of these methods on shapes of left caudate nucleus and left hippocampus. The training set of left caudate nucleus consisted of 26 data sets and the test set contained 3 volumes. Error between a particular shape representation and ground truth was calculated by computing the number of mislabeled voxels using each of the methods. Figure 1 gives the error using each of the methods. Similar tests were done on a training set of 20 hippocampus data with 3 test volumes. Figure 2 gives the error table for each of the methods [1].
Segmentation
Based on this representation, we derive a parametric active surface evolution using the multiscale prior coefficients as parameters for our optimization procedure to naturally include the prior for segmentation. Additionally, the optimization method can be applied in a coarse-to-fine manner.
Results
We applied our algorithm to the caudate nucleus, a brain structure of interest in the study of schizophrenia [2]. Our validation shows our algorithm is computationally efficient and outperforms the Active Shape Model (ASM) algorithm, by capturing finer shape details.
References
- [1] Nain D, Haker S, Bobick A, Tannenbaum A. Multiscale 3D Shape Analysis using Spherical Wavelets. Proc MICCAI, Oct 26-29 2005; p 459-467 [1]
- [2] Nain D, Haker S, Bobick A, Tannenbaum A. Shape-driven 3D Segmentation using Spherical Wavelets. Proc MICCAI, Oct 2-5, 2006. PDF of paper
Key Investigators
- Core 1:
- Georgia Tech: Delphine Nain, Aaron Bobick, Allen Tannenbaum
- Harvard SPL: Steven Haker
Collaborators
- Core 1: Martin Styner (UNC)
- Core 2: Jim Miller (GE), Luis Ibanez (Kitware)
- Core 3: James Levitt, Marc Niethammer, Sylvain Bouix, Martha Shenton (Harvard PNL)
Links:
- Paper presented in MICCAI 2006, Copenhagen, October 2 - 4, 2006
- Code: ITK Spherical Wavelet Transform Filter
- Georgia Tech Summary Page
- NA-MIC_Collaborations
Y. Rathi, S. Dambreville, and A. Tannenbaum. "Comparative Analysis of Kernel Methods for Statistical Shape Learning", In CVAMIA held in conjunction with ECCV, 2006.