Difference between revisions of "Projects:GeodesicTractographySegmentation"
| Line 1: | Line 1: | ||
| + | =Geodesic Active Contours for Fiber Tractography and Fiber Bundle Segmentation= | ||
| + | |||
Back to [[NA-MIC_Collaborations|NA-MIC_Collaborations]] | Back to [[NA-MIC_Collaborations|NA-MIC_Collaborations]] | ||
| − | |||
'''Objective:''' | '''Objective:''' | ||
| Line 10: | Line 11: | ||
''Fiber Tractography'' | ''Fiber Tractography'' | ||
| − | The goal of fiber tractography is to find open curves (i.e. paths without volume) in the white matter which correspond to something anatomically significant | + | The goal of fiber tractography is to find open curves (i.e. paths without volume) in the white matter which correspond to something anatomically significant. In our framework, a direction-dependent Finsler manifold is constructed. Note that Riemannian manifolds based on tensors comprise a subset of all possible Finsler manifolds and are most commonly used in this framework. Then, the best geodesic path connecting the input ROIs is computed on the manifold. This minimum cost geodesic curve is determined by solving a Hamilton-Jacobi-Bellman (HJB) equation using the Fast Sweeping algorithm. The resulting solution is the anchor tract connecting the two ROIs. |
| − | |||
| − | In our | ||
| − | |||
| − | |||
| − | + | Clinically speaking, the anchor tract has little meaning. However, during the computation of the anchor tract, connectivity maps are generated as a useful by-product which represent the connectivity of the brain volume to the input ROIs. | |
| − | + | Also, note that in this framework, special care is taken so that the minimum cost (or equivalently the fastest travel time of a particle moving along the curve in the given manifold) and the anisotropic front propagation used to solve the HJB equation are appropriately related through a Legendre transformation. Algorithms which inappropriately ignore the Legendre transformation can severely impact the anisotropy information in front propagation based PDE solvers. | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
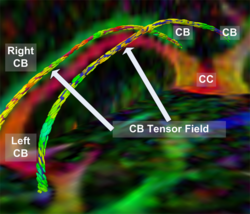
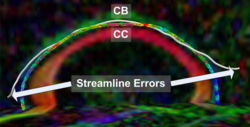
Recently, we have applied this method to the cingulum bundle, as shown in the following images: | Recently, we have applied this method to the cingulum bundle, as shown in the following images: | ||
| − | |||
| − | |||
{| | {| | ||
| Line 39: | Line 28: | ||
|} | |} | ||
| − | + | ''Fiber Bundle Segmentation'' | |
| − | + | We have developed a region-based active contour segmentation algorithm which provides volumetric fiber segmentations of fiber bundles. These active contours are initialized on the anchor tract and are expanded away from the anchor tract to capture the volumetric fiber bundle. | |
| − | + | ||
| − | + | ''Data'' | |
| − | |||
| − | |||
| + | We are using Harvard's high angular resolution datasets which currently consist of a population of 12 schizophrenics and 12 normal controls. | ||
| − | + | ''Associated Results'' | |
| − | + | For previous results showing comparisons of this framework to traditional streamline frameworks and results showing the application of this framework to the segmentation of blood vessels, see [[Algorithm:GATech:DWMRI_Geodesic_Active_Contours_Archive| Associated Results]]. | |
| − | |||
| − | |||
| − | |||
''Statistical Results'' | ''Statistical Results'' | ||
| − | We are currently investigating Cingulum Bundle fractional anisotropy (FA) differences between a population of 12 schizophrenics and 12 normal controls. We find the anchor tracts as described above and then compute statistics for FA inside a tube of radii 1-3mm centered on the anchor tract. So far using this method we have been unable to find a statistical difference between the normal controls and the schizophrenics. | + | We are currently investigating Cingulum Bundle fractional anisotropy (FA) differences between a population of 12 schizophrenics and 12 normal controls. We find the anchor tracts as described above and then compute statistics for FA inside a tube of radii 1-3mm centered on the anchor tract. So far using this method we have been unable to find a statistical difference between the normal controls and the schizophrenics. Once we have processed the entire population using our volumetric segmenter, we will rerun the statistics on the full fiber bundle. |
Download the current statistical results [[Media:ResultsAnchorTube.txt|here.]] (last updated 18/Apr/2007) | Download the current statistical results [[Media:ResultsAnchorTube.txt|here.]] (last updated 18/Apr/2007) | ||
| − | |||
''Project Status'' | ''Project Status'' | ||
| Line 67: | Line 51: | ||
''References:'' | ''References:'' | ||
| − | * V. Mohan, J. Melonakos, M. Niethammer, M. Kubicki, and A. Tannenbaum. Finsler Level Set Segmentation for Imagery in Oriented Domains. BMVC 2007 | + | * J. Melonakos, M. Niethammer, V. Mohan, M. Kubicki, J. Miller, and A. Tannenbaum. Locally-Constrained Region-Based Methods for DW-MRI Segmentation. MMBIA 2007 (in submission). |
| − | * J. Melonakos, V. Mohan, M. Niethammer, K. Smith, M. Kubicki, and A. Tannenbaum. Finsler Tractography for White Matter Connectivity Analysis of the Cingulum Bundle. MICCAI 2007 | + | * V. Mohan, J. Melonakos, M. Niethammer, M. Kubicki, and A. Tannenbaum. Finsler Level Set Segmentation for Imagery in Oriented Domains. BMVC 2007 (in press). |
| − | * J. Melonakos, E. Pichon, S. Angenet, and A. Tannenbaum. Finsler Active Contours. IEEE Transactions on Pattern Analysis and Machine Intelligence, | + | * J. Melonakos, V. Mohan, M. Niethammer, K. Smith, M. Kubicki, and A. Tannenbaum. Finsler Tractography for White Matter Connectivity Analysis of the Cingulum Bundle. MICCAI 2007 (in press). |
| + | * J. Melonakos, E. Pichon, S. Angenet, and A. Tannenbaum. Finsler Active Contours. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2007 (in press). | ||
* E. Pichon and A. Tannenbaum. Curve segmentation using directional information, relation to pattern detection. In IEEE International Conference on Image Processing (ICIP), volume 2, pages 794-797, 2005. | * E. Pichon and A. Tannenbaum. Curve segmentation using directional information, relation to pattern detection. In IEEE International Conference on Image Processing (ICIP), volume 2, pages 794-797, 2005. | ||
* E. Pichon, C-F Westin, and A. Tannenbaum. A Hamilton-Jacobi-Bellman approach to high angular resolution diffusion tractography. In International Conference on Medical Image Computing and Computer Assisted Intervention (MICCAI), pages 180-187, 2005. | * E. Pichon, C-F Westin, and A. Tannenbaum. A Hamilton-Jacobi-Bellman approach to high angular resolution diffusion tractography. In International Conference on Medical Image Computing and Computer Assisted Intervention (MICCAI), pages 180-187, 2005. | ||
Revision as of 21:06, 25 July 2007
Home < Projects:GeodesicTractographySegmentationGeodesic Active Contours for Fiber Tractography and Fiber Bundle Segmentation
Back to NA-MIC_Collaborations
Objective:
The purpose of this work is to extract white matter tracts and volumetric fiber bundles from Diffusion-Weighted MRI (DW-MRI) in order to study clinically relevant outcomes related to these structures. The idea is to use directional information in an anisotropic energy functional based on the Finsler metric (remember that the Riemannian metric is one particular Finsler metric of interest) in order to extract the best geodesic (i.e. optimal) path, which we dub "the anchor tract", between two regions of interest. Subsequently, region-based active contours are used to segment the associated volumetric fiber bundle. Finally, statistics are computed along both the anchor tract and the volumetric fiber bundle which may be used to compare different clinical populations.
Progress:
Fiber Tractography
The goal of fiber tractography is to find open curves (i.e. paths without volume) in the white matter which correspond to something anatomically significant. In our framework, a direction-dependent Finsler manifold is constructed. Note that Riemannian manifolds based on tensors comprise a subset of all possible Finsler manifolds and are most commonly used in this framework. Then, the best geodesic path connecting the input ROIs is computed on the manifold. This minimum cost geodesic curve is determined by solving a Hamilton-Jacobi-Bellman (HJB) equation using the Fast Sweeping algorithm. The resulting solution is the anchor tract connecting the two ROIs.
Clinically speaking, the anchor tract has little meaning. However, during the computation of the anchor tract, connectivity maps are generated as a useful by-product which represent the connectivity of the brain volume to the input ROIs.
Also, note that in this framework, special care is taken so that the minimum cost (or equivalently the fastest travel time of a particle moving along the curve in the given manifold) and the anisotropic front propagation used to solve the HJB equation are appropriately related through a Legendre transformation. Algorithms which inappropriately ignore the Legendre transformation can severely impact the anisotropy information in front propagation based PDE solvers.
Recently, we have applied this method to the cingulum bundle, as shown in the following images:
Fiber Bundle Segmentation
We have developed a region-based active contour segmentation algorithm which provides volumetric fiber segmentations of fiber bundles. These active contours are initialized on the anchor tract and are expanded away from the anchor tract to capture the volumetric fiber bundle.
Data
We are using Harvard's high angular resolution datasets which currently consist of a population of 12 schizophrenics and 12 normal controls.
Associated Results
For previous results showing comparisons of this framework to traditional streamline frameworks and results showing the application of this framework to the segmentation of blood vessels, see Associated Results.
Statistical Results
We are currently investigating Cingulum Bundle fractional anisotropy (FA) differences between a population of 12 schizophrenics and 12 normal controls. We find the anchor tracts as described above and then compute statistics for FA inside a tube of radii 1-3mm centered on the anchor tract. So far using this method we have been unable to find a statistical difference between the normal controls and the schizophrenics. Once we have processed the entire population using our volumetric segmenter, we will rerun the statistics on the full fiber bundle.
Download the current statistical results here. (last updated 18/Apr/2007)
Project Status
- Working 3D implementation in Matlab using the C-based Mex functions.
- Currently porting to ITK.
References:
- J. Melonakos, M. Niethammer, V. Mohan, M. Kubicki, J. Miller, and A. Tannenbaum. Locally-Constrained Region-Based Methods for DW-MRI Segmentation. MMBIA 2007 (in submission).
- V. Mohan, J. Melonakos, M. Niethammer, M. Kubicki, and A. Tannenbaum. Finsler Level Set Segmentation for Imagery in Oriented Domains. BMVC 2007 (in press).
- J. Melonakos, V. Mohan, M. Niethammer, K. Smith, M. Kubicki, and A. Tannenbaum. Finsler Tractography for White Matter Connectivity Analysis of the Cingulum Bundle. MICCAI 2007 (in press).
- J. Melonakos, E. Pichon, S. Angenet, and A. Tannenbaum. Finsler Active Contours. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2007 (in press).
- E. Pichon and A. Tannenbaum. Curve segmentation using directional information, relation to pattern detection. In IEEE International Conference on Image Processing (ICIP), volume 2, pages 794-797, 2005.
- E. Pichon, C-F Westin, and A. Tannenbaum. A Hamilton-Jacobi-Bellman approach to high angular resolution diffusion tractography. In International Conference on Medical Image Computing and Computer Assisted Intervention (MICCAI), pages 180-187, 2005.
Key Investigators:
- Georgia Tech: John Melonakos, Vandana Mohan, Sam Dambreville, Allen Tannenbaum
- Harvard/BWH: Marek Kubicki, Marc Niethammer, Kate Smith, C-F Westin, Martha Shenton
Links:
For some additional diffusion-related thoughts, see: DW-MRI Bird's Eye View.