Algorithm:GATech

Back to NA-MIC Algorithms

Overview of Georgia Tech Algorithms

At Georgia Tech, we are broadly interested in a range of mathematical image analysis algorithms for segmentation, registration, diffusion-weighted MRI analysis, and statistical analysis. For many applications, we cast the problem in an energy minimization framework wherein we define a partial differential equation whose numeric solution corresponds to the desired algorithmic outcome. The following are many examples of PDE techniques applied to medical image analysis.

Georgia Tech Projects

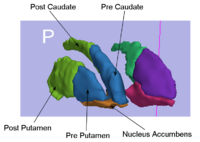
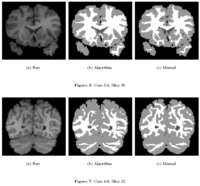
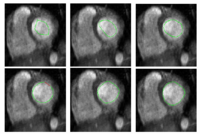
	Multiscale Shape Segmentation Techniques To represent multiscale variations in a shape population in order to drive the segmentation of deep brain structures, such as the caudate nucleus or the hippocampus. More... New: Delphine Nain won the best student paper at MICCAI 2006 in the category "Segmentation and Registration" for her paper entitled "Shape-driven surface segmentation using spherical wavelets" by D. Nain, S. Haker, A. Bobick, A. Tannenbaum.
	Geodesic Active Contours for Fiber Tractography and Fiber Bundle Segmentation In this work, we provide an energy minimization framework which allows one to find fiber tracts and volumetric fiber bundles in brain diffusion-weighted MRI (DW-MRI). More... New: J. Melonakos, E. Pichon, S. Angenet, and A. Tannenbaum. Finsler Active Contours. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2007 (in press).
	Optimal Mass Transport Registration The goal of this project is to implement a computationaly efficient Elastic/Non-rigid Registration algorithm based on the Monge-Kantorovich theory of optimal mass transport for 3D Medical Imagery. Our technique is based on Multigrid and Multiresolution techniques. This method is particularly useful because it is parameter free and utilizes all of the grayscale data in the image pairs in a symmetric fashion and no landmarks need to be specified for correspondence. More... New: Tauseef ur Rehman, A. Tannenbaum. Multigrid Optimal Mass Transport for Image Registration and Morphing. SPIE Conference on Computational Imaging V, Jan 2007.
	Rule-Based Segmentation Techniques In this work, we provide software to semi-automate the implementation of segmentation procedures based on expert neuroanatomist rules. More... New: Al-Hakim, et al. Parcellation of the Striatum. SPIE MI 2007.
	Conformal Flattening The goal of this project is for better visualizing and computation of neural activity from fMRI brain imagery. Also, with this technique, shapes can be mapped to shperes for shape analysis, registration or other purposes. Our technique is based on conformal mappings which map genus-zero surface: in fmri case cortical or other surfaces, onto a sphere in an angle preserving manner. More... New: Y. Gao, J. Melonakos, and A. Tannenbaum. Conformal Flattening ITK Filter. ISC/NA-MIC Workshop on Open Science at MICCAI 2006.
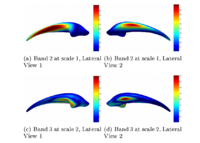
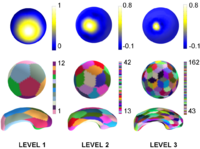
	Multiscale Shape Analysis We present a novel method of statistical surface-based morphometry based on the use of non-parametric permutation tests and a spherical wavelet (SWC) shape representation. More... New: D. Nain, M. Styner, M. Niethammer, J. J. Levitt, M E Shenton, G Gerig, A. Bobick, A. Tannenbaum. Statistical Shape Analysis of Brain Structures using Spherical Wavelets. Accepted in The Fourth IEEE International Symposium on Biomedical Imaging (ISBI ’07) that will be held April 12-15, 2007 in Metro Washington DC, USA.
	Kernel PCA for Segmentation Segmentation performances using active contours can be drastically improved if the possible shapes of the object of interest are learnt. The goal of this work is to use Kernel PCA to learn shape priors. Kernel PCA allows for learning non linear dependencies in data sets, leading to more robust shape priors. More... New: S. Dambreville, Y. Rathi, and A. Tannenbaum. A Framework for Image Segmentation using Image Shape Models and Kernel PCA Shape Priors. PAMI. Submitted to PAMI.
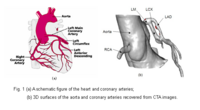
	Blood Vessel Segmentation The goal of this work is to develop blood vessel segmentation techniques for 3D MRI and CT data. The methods have been applied to coronary arteries and portal veins, with promising results. More... New: Y. Yang, S. George, D. Martin, A. Tannenbaum, and D. Giddens. 3D Modeling of Patient-Specific Geometries of Portal Veins Using MR Images. In Proceedings IEEE EMBS, 2006
	Knowledge-Based Bayesian Segmentation This ITK filter is a segmentation algorithm that utilizes Bayes's Rule along with an affine-invariant anisotropic smoothing filter. More... New: J. Melonakos, Y. Gao, and A. Tannenbaum. Tissue Tracking: Applications for Brain MRI Classification. SPIE Medical Imaging, 2007.
	Stochastic Methods for Segmentation New stochastic methods for implementing curvature driven flows for various medical tasks such as segmentation. More... New: Currently under investigation.
	KPCA, LLE, KLLE Shape Analysis The goal of this work is to study and compare shape learning techniques. The techniques considered are Linear Principal Components Analysis (PCA), Kernel PCA, Locally Linear Embedding (LLE) and Kernel LLE. More... New: Y. Rathi, S. Dambreville, and A. Tannenbaum. "Comparative Analysis of Kernel Methods for Statistical Shape Learning", In CVAMIA held in conjunction with ECCV, 2006.
	Statistical/PDE Methods using Fast Marching for Segmentation This Fast Marching based flow was added to Slicer 2. More...