Projects:DTISegmentation

Back to NA-MIC_Collaborations, MIT Algorithms

DTI Segmentation

Recent work shows that diffusion tensor imaging (DTI) can help resolving thalamic nuclei based on the characteristic fiber orientation of the corticothalamic/thalamocortical striations within each nucleus. In this project we develop a novel segmentation method based on spectral clustering.

With the new segmentation methods, we can resolve the organization of the thalamic nuclei into groups and subgroups solely based on the voxel affity matrix, avoiding the need for explicitly defined cluster centers. The identification of nuclear subdivisions can facilitate localization of functional activation and pathology to individual nuclear subgroups.

Further our methods do not make any assumptions specific to the thalamus, which could potentially allow us to expand our work to enable segmentation of other gray matter structures.

Description

Segmentation

We are using a modified spectral clustering algorithm to segment the thalamic data.

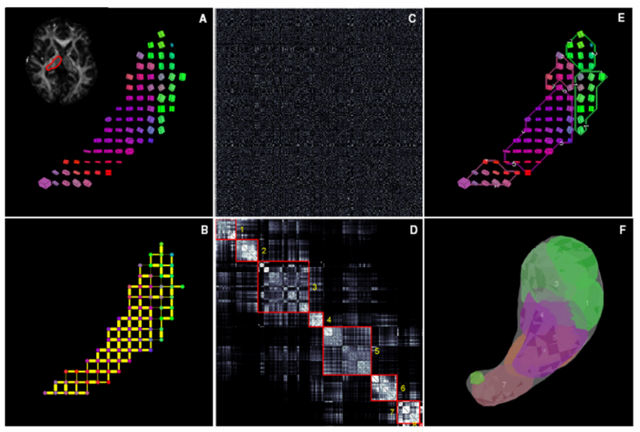
This image is a schematic outline of spectral segmentation algorithm. (A) DTI data from an individual thalamic hemisphere, shown here as a single slice cuboid map (B) Initial graph corresponding to the sparse affinity matrix (C) Unordered affinity matrix (D) Ordered and clustered affinity matrix (E) Clusters in the original data space (F) Clusters in 3D.

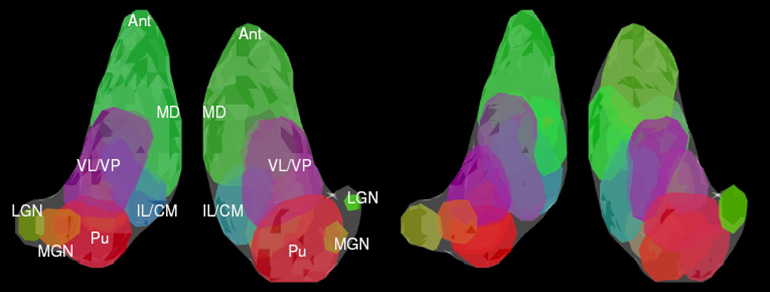
On the left there is a 3D rendering of expert segmentation of both hemispheres from one subject. On the right, it is the same subject segmented by the modified spectral clustering algorithm with 12 clusters. Clusters are colored according to their mean tensor orientations, therefore similar colors indicate similar mean tensor orientation.

Software

The algorithms now are implemented in matlab.

Key Investigators

MIT: Ulas Ziyan

UCLA: Jon Wisco

BWH: Carl-Fredrik Westin

Publications

NA-MIC Publications Database