Difference between revisions of "Projects:MultiscaleShapeSegmentation"
| Line 1: | Line 1: | ||
| − | + | Back to [[NA-MIC_Collaborations|NA-MIC_Collaborations]], [[Algorithm:GATech|Georgia Tech Algorithms]], [[Algorithm:UNC|UNC Algorithms]] | |
= Multiscale Shape Segmentation = | = Multiscale Shape Segmentation = | ||
| Line 30: | Line 30: | ||
= Publications = | = Publications = | ||
| − | + | ''In Print'' | |
| − | + | * [http://www.na-mic.org/Special:Publications?text=Multiscale++3D+Shape&submit=Search&words=all&title=checked&keywords=checked&authors=checked&abstract=checked&sponsors=checked&searchbytag=checked| NA-MIC Publications Database] | |
= Links = | = Links = | ||
Revision as of 04:30, 9 October 2007
Home < Projects:MultiscaleShapeSegmentationBack to NA-MIC_Collaborations, Georgia Tech Algorithms, UNC Algorithms
Multiscale Shape Segmentation
To represent multiscale variations in a shape population in order to drive the segmentation of deep brain structures, such as the caudate nucleus or the hippocampus.
Description
Shape Representation and Prior
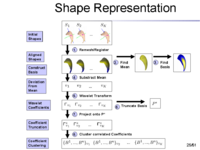
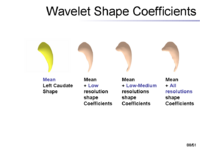
The overview of our shape representation is given in Figure 1. Our technique defines a multiscale parametric model of surfaces belonging to the same population using a compact set of spherical wavelets targeted to that population (Figure 2). We further refine the shape representation by separating into groups wavelet coefficients that describe independent global and/or local biological variations in the population, using spectral graph partitioning. We then learn a prior probability distribution induced over each group to explicitly encode these variations at different scales and spatial locations (Figure 4) [1].
Segmentation Based on this representation, we derive a parametric active surface evolution using the multiscale prior coefficients as parameters for our optimization procedure to naturally include the prior for segmentation. Additionally, the optimization method can be applied in a coarse-to-fine manner.
Results We applied our algorithm to the caudate nucleus, a brain structure of interest in the study of schizophrenia [2]. Our validation shows our algorithm is computationally efficient and outperforms the Active Shape Model (ASM) algorithm, by capturing finer shape details.
Key Investigators
- Georgia Tech: Delphine Nain, Aaron Bobick, Allen Tannenbaum
- UNC: Martin Styner
- GE: Jim Miller
- Kitware: Luis Ibanez
- Harvard SPL: Steven Haker, James Levitt, Marc Niethammer, Sylvain Bouix, Martha Shenton
Publications
In Print