Difference between revisions of "Projects:StochasticMethodsSegmentation"
| Line 7: | Line 7: | ||
''Introduction'' | ''Introduction'' | ||
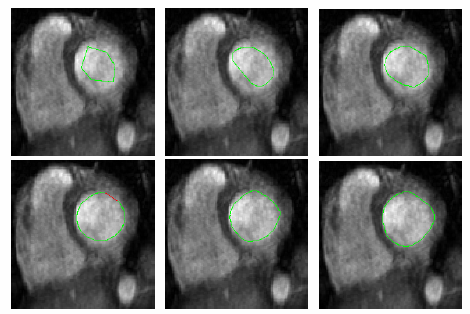
| − | + | We have continued our work on snakes using our stochastic framework. We can now generalize our results to an arbitrary Riemannian surface which includes the geodesic active contours as a special case. We are also implementing the directional flows based on the anisotropic conformal factor described above using this stochastic methodology. Our stochastic snakes models are based on the theory of interacting particle systems. This brings together the theories of curve evolution and hydrodynamic limits, and as such impacts our growing use of joint methods from probability and partial differential in image processing and computer vision. An example of a stochastic snake is illustrated in the Figure 1 below. | |
[[Image:Stochastic-snake.png|Figure 1: Stochastic Snake Evolution Example.]] | [[Image:Stochastic-snake.png|Figure 1: Stochastic Snake Evolution Example.]] | ||
| Line 18: | Line 18: | ||
* Georgia Tech: Delphine Nain, Samuel Dambreville, Tony Yezzi, Gozde Unal, Allen Tannenbaum | * Georgia Tech: Delphine Nain, Samuel Dambreville, Tony Yezzi, Gozde Unal, Allen Tannenbaum | ||
| − | |||
| − | |||
= Links = | = Links = | ||
Revision as of 04:38, 9 October 2007
Home < Projects:StochasticMethodsSegmentationBack to NA-MIC_Collaborations, Georgia Tech Algortihms
Stochastic Methods Segmentation
Our Objective is to develop new stochastic methods for implementing curvature driven flows for various medical tasks such as segmentation. This methodology will be used as an alternative to level set methods and has certain advantages including the ability to explicitly take into account noise models.
Introduction
We have continued our work on snakes using our stochastic framework. We can now generalize our results to an arbitrary Riemannian surface which includes the geodesic active contours as a special case. We are also implementing the directional flows based on the anisotropic conformal factor described above using this stochastic methodology. Our stochastic snakes models are based on the theory of interacting particle systems. This brings together the theories of curve evolution and hydrodynamic limits, and as such impacts our growing use of joint methods from probability and partial differential in image processing and computer vision. An example of a stochastic snake is illustrated in the Figure 1 below.
Progress
We now have working code written in C++ for the two dimensional case. We have worked out the stochastic model of the general geodesic active contour model.
Key Investigators
- Georgia Tech: Delphine Nain, Samuel Dambreville, Tony Yezzi, Gozde Unal, Allen Tannenbaum