Difference between revisions of "Projects:DTIFiberRegistration"
| Line 1: | Line 1: | ||
| + | = Joint Registration and Segmentation of DWI Fiber Tractography = | ||
| + | |||
| + | The purpose of this work is to jointly register and cluster DWI fiber tracts obtained from a group of subjects. We formulate a | ||
| + | maximum likelihood problem which the proposed method solves using a | ||
| + | generalized Expectation Maximization (EM) framework. Additionally, | ||
| + | the algorithm employs an outlier rejection and denoising strategy to | ||
| + | produce sharp probabilistic maps (an atlas) of certain bundles of interest. | ||
| + | This atlas is potentially useful for making diffusion measurements in | ||
| + | a common coordinate system to identify pathology related changes or | ||
| + | developmental trends. | ||
| + | |||
| + | = Description = | ||
| + | |||
| + | ''Initial Registration'' | ||
| + | |||
| + | A spatial normalization is necessary to obtain a group-wise | ||
| + | clustering of the resulting fibers. This initial normalization is performed | ||
| + | on the Fractional Anisotropy (FA) | ||
| + | images generated for each subject. This initial normalization aims | ||
| + | to remove gross differences across subjects due to global head size | ||
| + | and orientation. It is thus limited to a 9 parameter affine | ||
| + | transformation that accounts for scaling, rotation and translation. | ||
| + | The resulting transformations are then applied to each of the | ||
| + | computed fibers to map them into a common coordinate frame for | ||
| + | clustering. | ||
| + | |||
| + | ''Initial Fiber Clustering'' | ||
| + | |||
| + | Organization of tract fibers into bundles, in the entire white | ||
| + | matter, reveals anatomical connections such as the corpus callosum | ||
| + | and corona radiata. By clustering fibers from multiple subjects into | ||
| + | bundles, these common white matter structures can be discovered in | ||
| + | an automatic way, and the bundle models can be saved with expert | ||
| + | anatomical labels to form an atlas. In this work, | ||
| + | we take advantage of automatically segmented tractography that has been labeled (as | ||
| + | bundles) with such an atlas for initialization. | ||
| + | |||
| + | ''Joint Registration and Segmentation'' | ||
| + | |||
| + | Once we obtain an initial affine registration and clustering results using the high dimensional atlas, we iteratively fine-tune the registration and clustering results using a maximum likelihood framework, which is solved through a generalized EM algorithm. For the registration we use one set of affine parameters per fiber bundle, and combine these affine registrations into a single smooth and invertable warp field using a log-Euclidian poly-affine framework. Additionally, the algorithm employs an outlier rejection and denoising strategy while | ||
| + | producing sharp probabilistic maps of certain bundles of interest. | ||
| + | |||
| + | We tested the registration component of this algorithm without updating the clustering with 26 major fiber bundles. The results are shown in following image: | ||
| + | |||
| + | |||
| + | [[Image:FiberBundleReg.jpg]] | ||
| + | |||
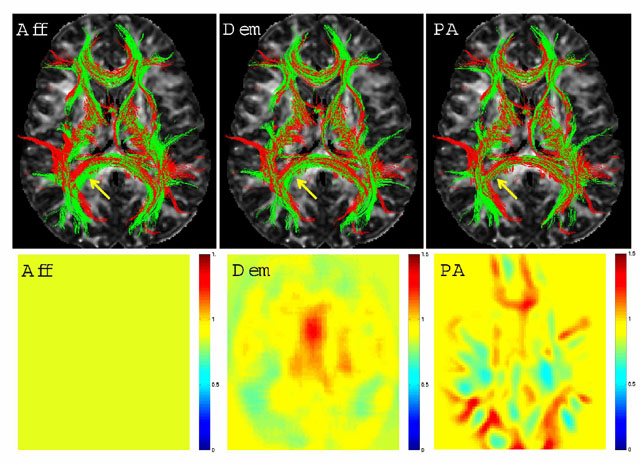
| + | Top Row: 3D renderings of the registered tracts of a | ||
| + | subject (in green) and the template (in red) within 5mm of the | ||
| + | central axial slice overlayed on the central FA slice of the | ||
| + | template. ''Aff'' (left) stands for the FA based global affine, | ||
| + | ''Dem'' (middle) for the demons algorithm and ''PA'' (right) for the | ||
| + | proposed framework in this work. Arrows point to an | ||
| + | area of differing qualities of registration. Overlapping of the red and | ||
| + | green fibers is indicative of better registration. Bottom Row: | ||
| + | Jacobian determinant images from the central slice of the volume: | ||
| + | Yellow represents areas with small changes in size, and the shades | ||
| + | of red and blue represent enlargement and shrinking, respectively. | ||
| + | The Jacobian of the global affine registration is constant. The | ||
| + | Jacobian of the demons algorithm is smooth due to the Gaussian | ||
| + | regularization. The Jacobian of the new algorithm reflects | ||
| + | the underlying anatomy because of the fiber bundle-based definition | ||
| + | of the deformation. | ||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
= Description = | = Description = | ||
Revision as of 19:54, 9 November 2007
Home < Projects:DTIFiberRegistrationContents
Joint Registration and Segmentation of DWI Fiber Tractography
The purpose of this work is to jointly register and cluster DWI fiber tracts obtained from a group of subjects. We formulate a maximum likelihood problem which the proposed method solves using a generalized Expectation Maximization (EM) framework. Additionally, the algorithm employs an outlier rejection and denoising strategy to produce sharp probabilistic maps (an atlas) of certain bundles of interest. This atlas is potentially useful for making diffusion measurements in a common coordinate system to identify pathology related changes or developmental trends.
Description
Initial Registration
A spatial normalization is necessary to obtain a group-wise clustering of the resulting fibers. This initial normalization is performed on the Fractional Anisotropy (FA) images generated for each subject. This initial normalization aims to remove gross differences across subjects due to global head size and orientation. It is thus limited to a 9 parameter affine transformation that accounts for scaling, rotation and translation. The resulting transformations are then applied to each of the computed fibers to map them into a common coordinate frame for clustering.
Initial Fiber Clustering
Organization of tract fibers into bundles, in the entire white matter, reveals anatomical connections such as the corpus callosum and corona radiata. By clustering fibers from multiple subjects into bundles, these common white matter structures can be discovered in an automatic way, and the bundle models can be saved with expert anatomical labels to form an atlas. In this work, we take advantage of automatically segmented tractography that has been labeled (as bundles) with such an atlas for initialization.
Joint Registration and Segmentation
Once we obtain an initial affine registration and clustering results using the high dimensional atlas, we iteratively fine-tune the registration and clustering results using a maximum likelihood framework, which is solved through a generalized EM algorithm. For the registration we use one set of affine parameters per fiber bundle, and combine these affine registrations into a single smooth and invertable warp field using a log-Euclidian poly-affine framework. Additionally, the algorithm employs an outlier rejection and denoising strategy while producing sharp probabilistic maps of certain bundles of interest.
We tested the registration component of this algorithm without updating the clustering with 26 major fiber bundles. The results are shown in following image:
Top Row: 3D renderings of the registered tracts of a subject (in green) and the template (in red) within 5mm of the central axial slice overlayed on the central FA slice of the template. Aff (left) stands for the FA based global affine, Dem (middle) for the demons algorithm and PA (right) for the proposed framework in this work. Arrows point to an area of differing qualities of registration. Overlapping of the red and green fibers is indicative of better registration. Bottom Row: Jacobian determinant images from the central slice of the volume: Yellow represents areas with small changes in size, and the shades of red and blue represent enlargement and shrinking, respectively. The Jacobian of the global affine registration is constant. The Jacobian of the demons algorithm is smooth due to the Gaussian regularization. The Jacobian of the new algorithm reflects the underlying anatomy because of the fiber bundle-based definition of the deformation.
Description
Collaborators: Ulas Ziyan (MIT), Lauren O'Donnell (BWH), Mert Sabuncu (MIT), Carl-Fredrik Westin (BWH)
Image registration is necessary to compare and combine information from a group of subjects. Affine registration (e.g. Talairach normalization) is common for group analysis, but this typically yields poor alignment accuracy in certain local regions of interest.
To address this, there has been interest in developing nonlinear registration methods. In nonlinear registration, the description and regularization of the deformation is critical, since an unconstrained registration algorithm suffers form the potential problem of overfitting to the images, which may undermine consecutive analyses. A popular approach is to employ a model-based regularization which may have no biological meaning. Yet, we believe that the regularization and description of the deformation should be grounded in the application.
In this project, we explore the use of anatomical structures (called fiber bundles) extracted from Diffusion MR Images of a group of subjects for regularizing a non-linear registration algorithm.
Segmentation
Organization of tract fibers into bundles, in the entire white matter, reveals anatomical connections such as the corpus callosum and corona radiata. By clustering fibers from multiple subjects into bundles, these common white matter structures can be discovered in an automatic way, and the bundle models can be saved with expert anatomical labels to form an atlas. In this work, we take advantage of automatically segmented tractography that has been labeled (as bundles) with such an atlas.
Registration of Fiber Bundles
To align the bundles from two subjects, we utilize the corresponce information from the segmentation results in order to compute a non-linear warp field. More details will be posted once this work is accepted for publication.
Top Row: 3D renderings of the registered tracts of a subject (in green) and the template (in red) within 5mm of the central axial slice overlayed on the central FA slice of the template. Aff (left) stands for the FA based global affine, Dem (middle) for the demons algorithm and PA (right) for the proposed framework in this work. Arrows point to an area of differing qualities of registration. Overlapping of the red and green fibers is indicative of better registration. Bottom Row: Jacobian determinant images from the central slice of the volume: Yellow represents areas with small changes in size, and the shades of red and blue represent enlargement and shrinking, respectively. The Jacobian of the global affine registration is constant. The Jacobian of the demons algorithm is smooth due to the Gaussian regularization. The Jacobian of the new algorithm reflects the underlying anatomy because of the fiber bundle-based definition of the deformation.
Publications
Submitted for publication.
Software
The algorithms now are implemented in matlab.