Algorithm:MIT:New

Back to NA-MIC Algorithms

Overview of MIT Algorithms

A brief overview of the MIT's algorithms goes here. This should not be much longer than a paragraph. Remember that people visiting your site want to be able to understand very quickly what you're all about and then they want to jump into your site's projects. The projects below are organized into a two column table: the left column is for representative images and the right column is for project overviews. The number of rows corresponds to the number of projects at your site. Put the most interesting and relevant projects at the top of the table. You do not need to organize the table according to subject matter (i.e. do not group all segmentation projects together and all DWI projects together).

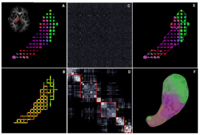
Shape Based Segmentation and Registration

Effects of Registration Regularization on Segmentation Accuracy

Multimodal Atlas

Shape Analysis With Overcomplete Wavelets

fMRI clustering

Joint Registration and Segmentation of DWI Fiber Tractography

Shape Based Level Segmentation

DTI Fiber Clustering and Fiber-Based Analysis

Fiber Tract Modeling, Clustering and Quantitative Analysis

DTI-based Segmentation

Stochastic Tractography

fMRI Detection and Analysis

Population Analysis of Anatomical Variability

Groupwise Registration

MIT Projects

	Shape Based Segmentation and Registration This type of algorithms assigns a tissue type to each voxel in the volume. Incorporating prior shape information biases the label assignment towards contiguous regions that are consistent with the shape model. More... New: K.M. Pohl, J. Fisher, S. Bouix, M. Shenton, R. W. McCarley, W.E.L. Grimson, R. Kikinis, and W.M. Wells. Using the Logarithm of Odds to Define a Vector Space on Probabilistic Atlases. Accepted to the Special Issue of Best Selected Papers from MICCAI 06 in Medical Image Analysis More...
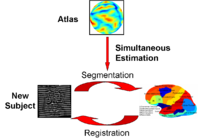
	Optimal Atlas Regularization in Image Segmentation We propose a unified framework for computing atlases from manually labeled data sets at various degrees of “sharpness” and the joint registration and segmentation of a new brain with these atlases. Using this framework, we investigate the tradeoff between warp regularization and image fidelity, i.e. the smoothness of the new subject warp and the sharpness of the atlas in a segmentation application. More... New: B.T.T. Yeo, M.R. Sabuncu, R. Desikan, B. Fischl, P. Golland. Effects of Registration Regularization and Atlas Sharpness on Segmentation Accuracy. In Proceedings of MICCAI: International Conference on Medical Image Computing and Computer Assisted Intervention, 683-691, 2007. MICCAI Young Scientist Award.
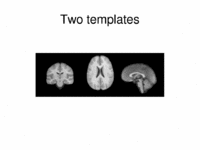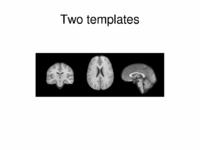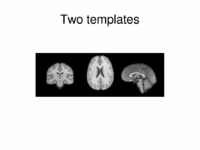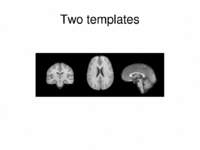
	Multimodal Atlas In this work, we propose and investigate an algorithm that jointly co-registers a collection of images while computing multiple templates. The algorithm, called iCluster, is used to compute multiple atlases for a given population. More... New: M.R. Sabuncu, M.E. Shenton, P. Golland. Joint Registration and Clustering of Images. In Proceedings of MICCAI 2007 Statistical Registration Workshop: Pair-wise and Group-wise Alignment and Atlas Formation, 47-54, 2007. More...
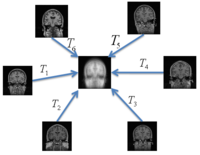
	Groupwise Registration We are exploring algorithms for groupwise registration of medical data. More... New: Serdar K Balci, Polina Golland, Sandy Wells, Lilla Zollei, Mert R Sabuncu and Kinh Tieu. Groupwise registration of medical data.
	Shape Analysis With Overcomplete Wavelets In this work, we extend the Euclidean wavelets to the sphere. The resulting over-complete spherical wavelets are invariant to the rotation of the spherical image parameterization. We apply the over-complete spherical wavelet to cortical folding development More... New: B.T.T. Yeo, W. Ou, P. Golland. On the Construction of Invertible Filter Banks on the 2-Sphere. Yeo, Ou and Golland. Accepted to the IEEE Transactions on Image Processing. P. Yu, B.T.T. Yeo, P.E. Grant, B. Fischl, P. Golland. Cortical Folding Development Study based on Over-Complete Spherical Wavelets. In Proceedings of MMBIA: IEEE Computer Society Workshop on Mathematical Methods in Biomedical Image Analysis, 2007. More...
	fMRI clustering This type of algorithms assigns a tissue type to each voxel in the volume. Incorporating prior shape information biases the label assignment towards contiguous regions that are consistent with the shape model. More... New: K.M. Pohl, J. Fisher, S. Bouix, M. Shenton, R. W. McCarley, W.E.L. Grimson, R. Kikinis, and W.M. Wells. Using the Logarithm of Odds to Define a Vector Space on Probabilistic Atlases. Accepted to the Special Issue of Best Selected Papers from MICCAI 06 in Medical Image Analysis More...
	Joint Registration and Segmentation of DWI Fiber Tractography The goal of this work is to jointly register and cluster DWI fiber tracts obtained from a group of subjects. More... New: U. Ziyan, M. R. Sabuncu, W. E. L. Grimson, Carl-Fredrik Westin. A Robust Algorithm for Fiber-Bundle Atlas Construction. MMBIA 2007
	Shape Based Level Segmentation This class of algorithms explicitly manipulates the representation of the object boundary to fit the strong gradients in the image, indicative of the object outline. Bias in the boundary evolution towards the likely shapes improves the robustness of the segmentation results when the intensity information alone is insufficient for boundary detection. More... New:
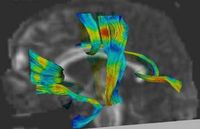
	DTI Fiber Clustering and Fiber-Based Analysis The goal of this project is to provide structural description of the white matter architecture as a partition into coherent fiber bundles and clusters, and to use these bundles for quantitative measurement. More... New: Monica E. Lemmond, Lauren J. O'Donnell, Stephen Whalen, Alexandra J. Golby. Characterizing Diffusion Along White Matter Tracts Affected by Primary Brain Tumors. Accepted to HBM 2007.
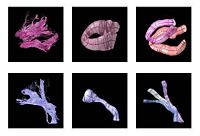
	Fiber Tract Modeling, Clustering, and Quantitative Analysis The goal of this work is to model the shape of the fiber bundles and use this model discription in clustering and statistical analysis of fiber tracts. More... New: M. Maddah, W. M. Wells, S. K. Warfield, C.-F. Westin, and W. E. L. Grimson, Probabilistic Clustering and Quantitative Analysis of White Matter Fiber Tracts,IPMI 2007, Netherlands.
	DTI-based Segmentation Unlike conventional MRI, DTI provides adequate contrast to segment the thalamic nuclei, which are gray matter structures. More... New: Ulas Ziyan, David Tuch, Carl-Fredrik Westin. Segmentation of Thalamic Nuclei from DTI using Spectral Clustering. Accepted to MICCAI 2006.
	Stochastic Tractography This work calculates posterior distributions of white matter fiber tract parameters given diffusion observations in a DWI volume. More... New:
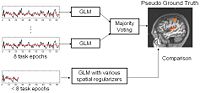
	fMRI Detection and Analysis We are exploring algorithms for improved fMRI detection and interpretation by incorporting spatial priors and anatomical information to guide the detection. More... New: Wanmei Ou, Sandy Wells, Polina Golland. Bridging Spatial Regularization And Anatomical Priors in fMRI Detection. In preparation for submission to IEEE TMI.
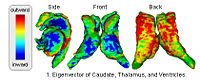
	Population Analysis of Anatomical Variability Our goal is to develop mathematical approaches to modeling anatomical variability within and across populations using tools like local shape descriptors of specific regions of interest and global constellation descriptors of multiple ROI's. More... New: Mert R Sabuncu and Polina Golland. Structural Constellations for Population Analysis of Anatomical Variability.