Difference between revisions of "Projects:fMRIClustering"
| Line 21: | Line 21: | ||
''Generative Model for Functional Connectivity'' | ''Generative Model for Functional Connectivity'' | ||
| + | |||
| + | In the classical functional connectivity analysis, networks of interest are | ||
| + | defined based on correlation with the mean time course of a user-selected | ||
| + | `seed' region. Further, the user has to also specify a subject-specific threshold at which correlation | ||
| + | values are deemed significant. In this project, we simultaneously estimate the optimal | ||
| + | representative time courses that summarize the fMRI data well and | ||
| + | the partition of the volume into a set of disjoint regions that are best | ||
| + | explained by these representative time courses. This approach to functional connectivity analysis offers two | ||
| + | advantages. First, is removes the sensitivity of the analysis to the details | ||
| + | of the seed selection. Second, it substantially simplifies group analysis | ||
| + | by eliminating the need for the subject-specific threshold. Our experimental results indicate that | ||
| + | the functional segmentation provides a robust, anatomically meaningful | ||
| + | and consistent model for functional connectivity in fMRI. | ||
We formulate the problem of characterizing connectivity as a partition of voxels into subsets that are well characterized by a certain number of representative hypotheses, or time courses, based on the similarity of their time courses to each hypothesis. We model the fMRI signal at each voxel as generated by a mixture of Gaussian distributions whose centers are the desired representative time courses. Using the EM algorithm to solve the corresponding model-fitting problem, we alternatively estimate the representative time courses and cluster assignments to improve our random initialization. | We formulate the problem of characterizing connectivity as a partition of voxels into subsets that are well characterized by a certain number of representative hypotheses, or time courses, based on the similarity of their time courses to each hypothesis. We model the fMRI signal at each voxel as generated by a mixture of Gaussian distributions whose centers are the desired representative time courses. Using the EM algorithm to solve the corresponding model-fitting problem, we alternatively estimate the representative time courses and cluster assignments to improve our random initialization. | ||
| − | ''Experimental | + | ''Experimental Results'' |
We used data from 7 subjects with a diverse set of visual experiments including localizer, morphing, rest, internal tasks, and movie. The functional scans were pre-processed for motion artifacts, manually aligned into the Talairach coordinate system, detrended (removing linear trends in the | We used data from 7 subjects with a diverse set of visual experiments including localizer, morphing, rest, internal tasks, and movie. The functional scans were pre-processed for motion artifacts, manually aligned into the Talairach coordinate system, detrended (removing linear trends in the | ||
baseline activation) and smoothed (8mm kernel). | baseline activation) and smoothed (8mm kernel). | ||
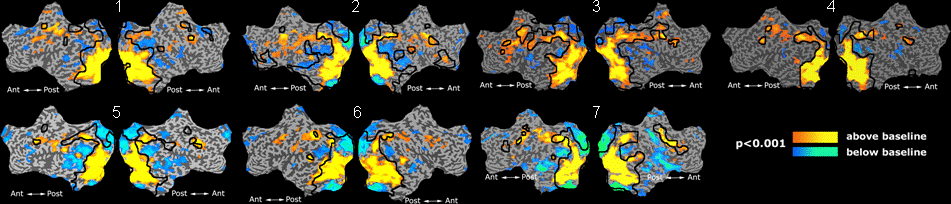
| − | + | Fig. 1 shows the 2-system partition extracted in each subject independently | |
| − | + | of all others. It also displays the boundaries of the intrinsic system determined | |
| − | + | through the traditional seed selection, showing good agreement between the two | |
| − | + | partitions. Fig.2 presents the group average of the subject-specific 2-system maps. Color shading shows the proportion of subjects whose clustering agreed with the majority label. | |
{| | {| | ||
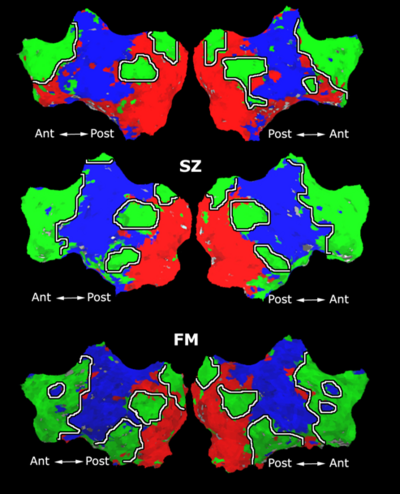
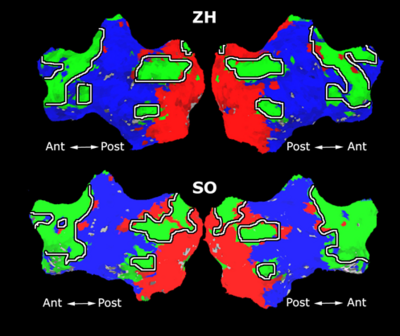
| − | |+ '''Fig | + | |+ '''Fig 1. 2-System Parcelation. Results for all 7 subjects.''' |
|valign="top"|[[Image:mit_fmri_clustering_parcellation2_shb1_4.png |400px]] | |valign="top"|[[Image:mit_fmri_clustering_parcellation2_shb1_4.png |400px]] | ||
|- | |- | ||
| Line 42: | Line 55: | ||
|valign="top"|[[Image:mit_fmri_clustering_parcellation2_shb7.png |400px]] | |valign="top"|[[Image:mit_fmri_clustering_parcellation2_shb7.png |400px]] | ||
|} | |} | ||
| + | |||
| + | {| | ||
| + | |+ '''Fig 2. 2-System Parcellation. Group-wise result.''' | ||
| + | |valign="top"|[[Image:mit_fmri_clustering_parcellation2_xsub.png |thumb|700px]] | ||
| + | |} | ||
| + | |||
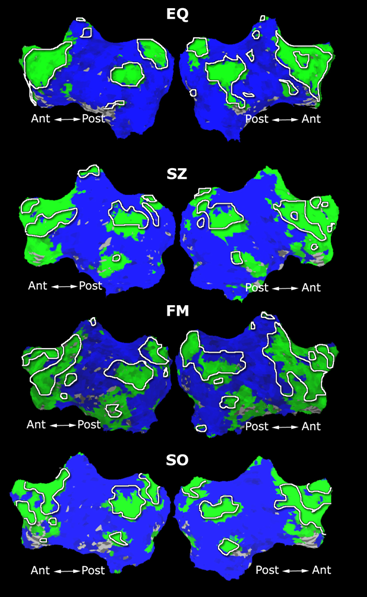
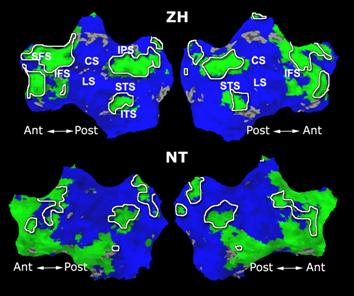
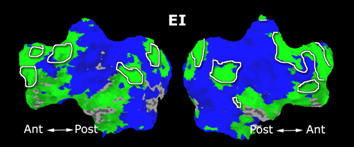
| + | Fig. 3 shows the results of further clustering the stimulus-driven cluster into two clusters independently for each subject. In order to present a validation of the method, we compare these results with the conventional scheme for detection of visually responsive areas. In Fig. 4, color shows the statistical parametric map while solid lines indicate the boundaries of the visual system obtained through clustering. The results illustrate the agreement between the two methods. | ||
{| | {| | ||
Revision as of 23:07, 9 November 2007
Home < Projects:fMRIClusteringBack to NA-MIC_Collaborations, MIT Algorithms
fMRI Clustering
In the classical functional connectivity analysis, networks of interest are defined based on correlation with the mean time course of a user-selected `seed' region. Further, the user has to also specify a subject-specific threshold at which correlation values are deemed significant. In this project, we simultaneously estimate the optimal representative time courses that summarize the fMRI data well and the partition of the volume into a set of disjoint regions that are best explained by these representative time courses. This approach to functional connectivity analysis offers two advantages. First, is removes the sensitivity of the analysis to the details of the seed selection. Second, it substantially simplifies group analysis by eliminating the need for the subject-specific threshold. Our experimental results indicate that the functional segmentation provides a robust, anatomically meaningful and consistent model for functional connectivity in fMRI.
Currently, we are investigating the application of such clustering algorithms in detection of functional connectivity in high-level
Description
Generative Model for Functional Connectivity
In the classical functional connectivity analysis, networks of interest are defined based on correlation with the mean time course of a user-selected `seed' region. Further, the user has to also specify a subject-specific threshold at which correlation values are deemed significant. In this project, we simultaneously estimate the optimal representative time courses that summarize the fMRI data well and the partition of the volume into a set of disjoint regions that are best explained by these representative time courses. This approach to functional connectivity analysis offers two advantages. First, is removes the sensitivity of the analysis to the details of the seed selection. Second, it substantially simplifies group analysis by eliminating the need for the subject-specific threshold. Our experimental results indicate that the functional segmentation provides a robust, anatomically meaningful and consistent model for functional connectivity in fMRI.
We formulate the problem of characterizing connectivity as a partition of voxels into subsets that are well characterized by a certain number of representative hypotheses, or time courses, based on the similarity of their time courses to each hypothesis. We model the fMRI signal at each voxel as generated by a mixture of Gaussian distributions whose centers are the desired representative time courses. Using the EM algorithm to solve the corresponding model-fitting problem, we alternatively estimate the representative time courses and cluster assignments to improve our random initialization.
Experimental Results
We used data from 7 subjects with a diverse set of visual experiments including localizer, morphing, rest, internal tasks, and movie. The functional scans were pre-processed for motion artifacts, manually aligned into the Talairach coordinate system, detrended (removing linear trends in the baseline activation) and smoothed (8mm kernel).
Fig. 1 shows the 2-system partition extracted in each subject independently of all others. It also displays the boundaries of the intrinsic system determined through the traditional seed selection, showing good agreement between the two partitions. Fig.2 presents the group average of the subject-specific 2-system maps. Color shading shows the proportion of subjects whose clustering agreed with the majority label.
|
|
|
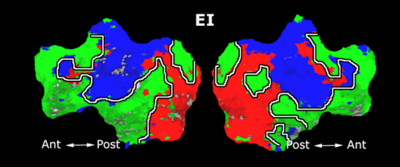
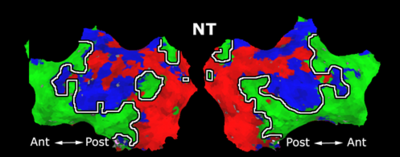
Fig. 3 shows the results of further clustering the stimulus-driven cluster into two clusters independently for each subject. In order to present a validation of the method, we compare these results with the conventional scheme for detection of visually responsive areas. In Fig. 4, color shows the statistical parametric map while solid lines indicate the boundaries of the visual system obtained through clustering. The results illustrate the agreement between the two methods.
|
|
|
|
Project Status
- Working 3D implementation in Matlab using the C-based Mex functions.
- Currently porting to ITK. (last updated 18/Apr/2007)
Key Investigators
- MIT: Danial Lashkari, Polina Golland, Nancy Kanwisher
Publications
In print
- P. Golland, Y. Golland, R. Malach. Detection of Spatial Activation Patterns As Unsupervised Segmentation of fMRI Data. In Proceedings of MICCAI: International Conference on Medical Image Computing and Computer Assisted Intervention, 110-118, 2007.
In press
- D. Lashkari, P. Golland. Convex Clustering with Exemplar-Based Models. In NIPS: Advances in Neural Information Processing Systems, 2007.