Projects:ParticlesForShapesAndComplexes

Back to NA-MIC Collaborations, Utah Algorithms

Adaptive, Particle-Based Sampling for Shapes and Complexes

This research is a new method for constructing compact statistical point-based models of ensembles of similar shapes that does not rely on any specific surface parameterization. The method requires very little preprocessing or parameter tuning, and is applicable to a wider range of problems than existing methods, including nonmanifold surfaces and objects of arbitrary topology.

Description

The proposed method is to construct a point-based sampling of the shape ensemble that simultaneously maximizes both the geometric accuracy and the statistical simplicity of the model. Surface point samples, which also define the shape-to-shape correspondences, are modeled as sets of dynamic particles that are constrained to lie on a set of implicit surfaces. Sample positions are optimized by gradient descent on an energy function that balances the negative entropy of the distribution on each shape with the positive entropy of the ensemble of shapes. We also extend the method with a curvature-adaptive sampling strategy in order to better approximate the geometry of the objects. We have developed code based on ITK for computation of correspondence-based models, and have validated out method in several papers against several synthetic and real examples in two and three dimensions, including application to the statistical shape analysis of brain structures. We used hippocampus data from a schizo-typal personality disorder (SPD) study funded by the Stanley Foundation and UNC-MHNCRC (MH33127), and caudate data from a schizophrenia study funded by NIMH R01 MH 50740 (Shenton), NIH K05 MH 01110 (Shenton), NIMH R01 MH 52807 (McCarley), and a VA Merit Award (Shenton).

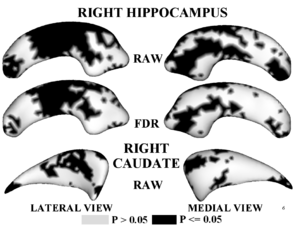
Figure 1,2 illustrates results of hypothesis testing for group differences from the control population for the left/right hippocampus and the left/right caudate. Raw and FDR-corrected p-values are given. Areasof significant group differences (p <= 0.05) are shown as dark regions. Areas with insignificant group differences (p > 0.05) are shown as light regions. Our results correlate with with other published hypothesis testing results on this data.

Our most recent work is in the application of the particle method to multi-object shape complexes. We have developed a novel method for computing surface point correspondences of multi-object anatomy that is a straightforward extension of the particle method for single-object anatomy. The correspondences take advantage of the statistical structure of an ensemble of complexes, and thus they are suitable for joint statistical analyses of shape and relative pose. The proposed method uses a dynamic particle system to optimize correspondence point positions across all structures in a complex simultaneously, in order to create a compact model of ensemble statistics. It is a different approach from previous methods for dealing with shape complexes, because to date researchers have considered the correspondence problem only for each structure independently, and have ignored intermodel correlations in the shape parameterization. These correlations are particularly important when the correspondences are constructed in order to reduce or minimize the information content of the ensemble.

Figure 1

Figure 2

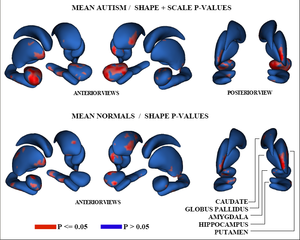
We have developed a formulation of the multi-object correspondence optimization, and have applied it to a proof-of-concept application to the analysis of brain structure complexes from a longitudinal study of pediatric autism that is underway at UNC Chapel Hill. This work is in conjunction with Martin Styner, Heather Cody Hazlett, and Joe Piven. Figure 3 shows the raw p-values from hypothesis testing for group differences as color-maps on mean shapes of the autism group (top row) and the normal control group (bottom row). Red indicates areas where significant group differences were found (p < 0.05), with blue elsewhere (p >= 0.05). The top row shows the results when relative geometric scale is included, and the bottom shows relative scale removed. Structures are shown in the their mean orientations, positions, and scale in the global coordinate frame. We computed the average orientation for each structure using methods for averaging in curved spaces.

Figure 3

Key Investigators

Josh Cates, Tom Fletcher, Ross Whitaker

Publications

In Print

• NA-MIC Publications Database