Difference between revisions of "Projects:SphericalDemons"
| Line 7: | Line 7: | ||
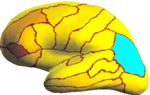
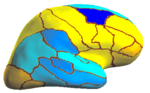
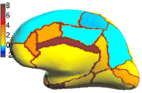
registration algorithm. We validate the technique in two different settings: (1) parcellation in a set of in-vivo cortical surfaces and (2) Brodmann area localization in ex-vivo cortical surfaces. | registration algorithm. We validate the technique in two different settings: (1) parcellation in a set of in-vivo cortical surfaces and (2) Brodmann area localization in ex-vivo cortical surfaces. | ||
| − | = Description | + | = Description |
| + | Motivated by the spherical representation of the cerebral cortex, this work deals with the problem of registering spherical images. Cortical folding patterns are correlated with both cytoarchitectural and functional regions. In group studies of cortical structure and function, determining corresponding folds across subjects is therefore important. | ||
| + | Unfortunately, many spherical warping algorithms are computationally expensive. One reason is the need for invertible deformations that preserve the topology of structural or functional regions across subjects. In this paper, we take the approach, previously demonstrated in the Euclidean space, of restricting the deformation space to be a composition of diffeomorphisms, each of which is | ||
| + | parameterized by a stationary velocity field. In each iteration, the algorithm greedily seeks the best diffeomorphism to be composed with the current transformation, resulting in much faster updates. | ||
| + | |||
| + | Another challenge in registration is the tradeoff between the image similarity measure and the regularization in the objective function. Since most regularizations favor smooth deformations, the gradient computation is complicated by the need to take into account the deformation in neighboring regions. For Euclidean images, the demons objective function facilitates a fast two-step optimization where the second step handles the warp regularization via a single convolution with a smoothing filter. Based on spherical vector spline interpolation theory and other differential geometric tools, we show that the two-stage optimization procedure of the demons algorithm can be efficiently applied on the sphere. | ||
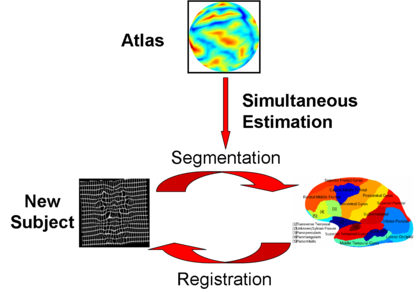
[[Image:RegSeg.png|center|400px|]] | [[Image:RegSeg.png|center|400px|]] | ||
Revision as of 20:04, 9 October 2008
Home < Projects:SphericalDemonsBack to NA-MIC Collaborations, MIT Algorithms
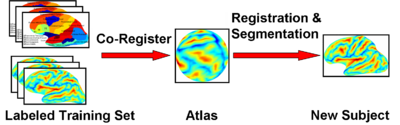
We present the fast Spherical Demons algorithm for registering two spherical images. By exploiting spherical vector spline interpolation theory, we show that a large class of regularizers for the modified demons objective function can be efficiently implemented on the sphere using convolution. Based on the one parameter subgroups of diffeomorphisms, the resulting registration is diffeomorphic and fast -- registration of two cortical mesh models with more than 100k nodes takes less than 5 minutes, comparable to the fastest surface registration algorithms. Moreover, the accuracy of our method compares favorably to the popular FreeSurfer registration algorithm. We validate the technique in two different settings: (1) parcellation in a set of in-vivo cortical surfaces and (2) Brodmann area localization in ex-vivo cortical surfaces.
= Description Motivated by the spherical representation of the cerebral cortex, this work deals with the problem of registering spherical images. Cortical folding patterns are correlated with both cytoarchitectural and functional regions. In group studies of cortical structure and function, determining corresponding folds across subjects is therefore important.
Unfortunately, many spherical warping algorithms are computationally expensive. One reason is the need for invertible deformations that preserve the topology of structural or functional regions across subjects. In this paper, we take the approach, previously demonstrated in the Euclidean space, of restricting the deformation space to be a composition of diffeomorphisms, each of which is parameterized by a stationary velocity field. In each iteration, the algorithm greedily seeks the best diffeomorphism to be composed with the current transformation, resulting in much faster updates.
Another challenge in registration is the tradeoff between the image similarity measure and the regularization in the objective function. Since most regularizations favor smooth deformations, the gradient computation is complicated by the need to take into account the deformation in neighboring regions. For Euclidean images, the demons objective function facilitates a fast two-step optimization where the second step handles the warp regularization via a single convolution with a smoothing filter. Based on spherical vector spline interpolation theory and other differential geometric tools, we show that the two-stage optimization procedure of the demons algorithm can be efficiently applied on the sphere.
Experimental Results
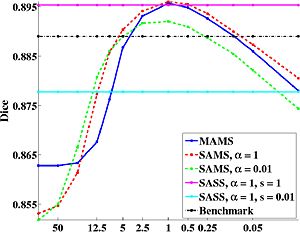
We use dice as the measure of segmentation quality. From the graph below, we note that the optimal algorithms correspond to a unique balance between atlas “sharpness” and warp regularization. Our experiments show that the optimal parameter values that correspond to this balance can be determined using cross-validation. The optimal parameter values are robust across subjects, and the same for both co-registration of the training data and registration of a new subject. This suggests that a single atlas at an optimal sharpness is sufficient to achieve the best segmentation results. Furthermore, our experiments also suggest that segmentation accuracy is tolerant up to a small mismatch between atlas sharpness and warp smoothness.
In the figure below, we display the percentage improvement of SASS over FreeSurfer [1,2]. For each of the 35 structures for each hemisphere, we perform a one-sided paired-sampled t-test between SASS and FreeSurfer, where each subject is considered a sample. We use the False Discovery Rate (FDR) to correct for multiple comparisons. In the left hemisphere, SASS achieves statistically significant improvement over FreeSurfer for 17 structures (FDR < 0.05), while the remaining structures yield no statistical difference. In the right hemisphere, SASS achieves improvement for 11 structures (FDR < 0.05), while the remaining structures yield no statistical difference. The p-values for the left and right hemispheres are pooled together for the False Discovery Rate analysis.
[1] Fischl, Sereno and Dale. High-resolution intersubject averaging and a coordinate system for the cortical surface. Human Brain Mapping, 8(4):272--284, 1999
[2] Fischl, van der Kouwe, Destrieux, Halgren, Segonne, Salat, Busa, Seidman, Goldstein, Kennedy, Caviness, Makris, Rosen and Dale. Automatically Parcellating the Human cerebral Cortex. Cerebral Cortex, 14:11--22, 2004
Key Investigators
- MIT Algorithms: [| B.T. Thomas Yeo], Mert Sabuncu, Rahul Desikan, Bruce Fischl, Polina Golland
Publications
In Print
In Press
- B.T.T. Yeo, M.R. Sabuncu, R. Desikan, B. Fischl, P. Golland. "Effects of Registration Regularization and Atlas Sharpness on Segmentation Accuracy". Accepted to Medical Image Analysis, 2008.