Projects:fMRIClustering

Back to NA-MIC Collaborations, MIT Algorithms

fMRI Clustering

One of the major goals in analysis of fMRI data is the detection of networks in the brain with similar functional behavior. A wide variety of methods including hypothesis-driven statistical tests, unsupervised learning methods such as PCA and ICA, and different clustering algorithms have been employed to find these networks. This project aims to particularly study application of model-based clustering algorithms in identification of functional connectivity in the brain.

Description

Generative Model for Functional Connectivity

In the classical functional connectivity analysis, networks of interest are defined based on correlation with the mean time course of a user-selected `seed' region. Further, the user has to also specify a subject-specific threshold at which correlation values are deemed significant. In this project, we simultaneously estimate the optimal representative time courses that summarize the fMRI data well and the partition of the volume into a set of disjoint regions that are best explained by these representative time courses. This approach to functional connectivity analysis offers two advantages. First, is removes the sensitivity of the analysis to the details of the seed selection. Second, it substantially simplifies group analysis by eliminating the need for the subject-specific threshold. Our experimental results indicate that the functional segmentation provides a robust, anatomically meaningful and consistent model for functional connectivity in fMRI.

We formulate the problem of characterizing connectivity as a partition of voxels into subsets that are well characterized by a certain number of representative hypotheses, or time courses, based on the similarity of their time courses to each hypothesis. We model the fMRI signal at each voxel as generated by a mixture of Gaussian distributions whose centers are the desired representative time courses. Using the EM algorithm to solve the corresponding model-fitting problem, we alternatively estimate the representative time courses and cluster assignments to improve our random initialization.

Experimental Results

We used data from 7 subjects with a diverse set of visual experiments including localizer, morphing, rest, internal tasks, and movie. The functional scans were pre-processed for motion artifacts, manually aligned into the Talairach coordinate system, detrended (removing linear trends in the baseline activation) and smoothed (8mm kernel).

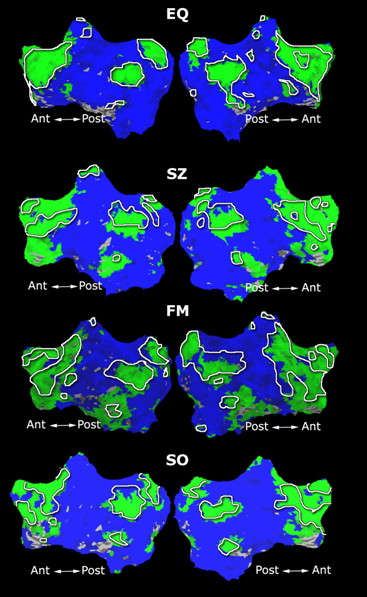
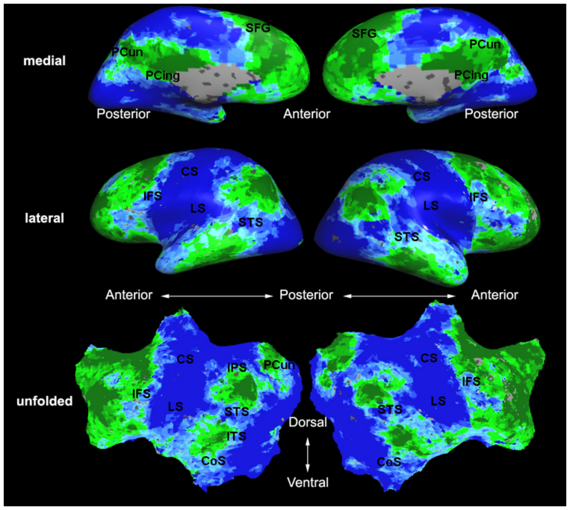
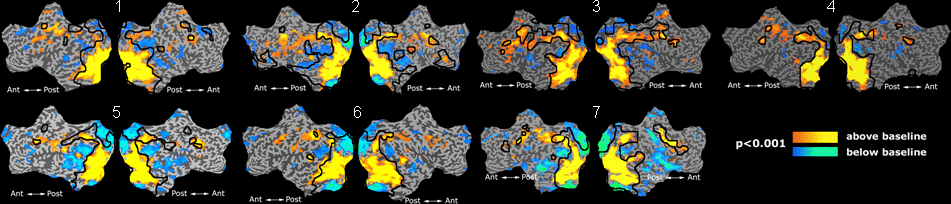
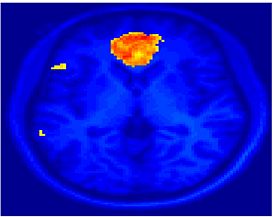
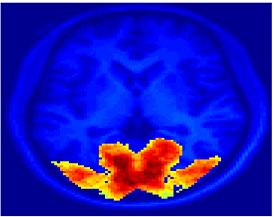
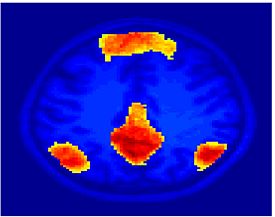
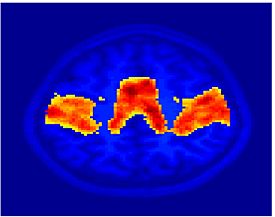
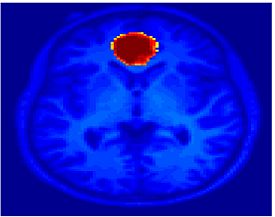
Fig. 1 shows the 2-system partition extracted in each subject independently of all others. It also displays the boundaries of the intrinsic system determined through the traditional seed selection, showing good agreement between the two partitions. Fig. 2 presents the results of further clustering the stimulus-driven cluster into two clusters independently for each subject.

Fig 1. 2-System Parcelation. Results for all 7 subjects.	Fig 2. 3-System Parcelation. Results for all 7 subjects.

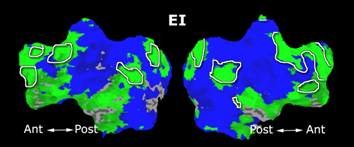
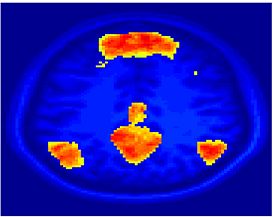
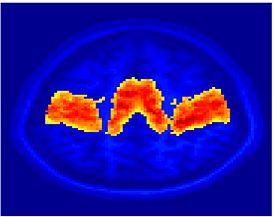
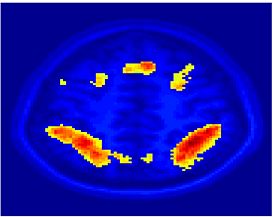
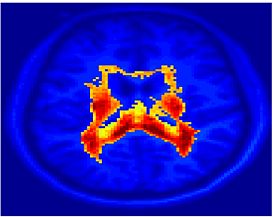
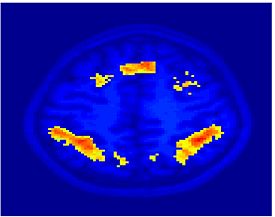
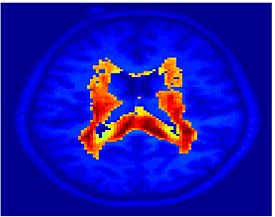
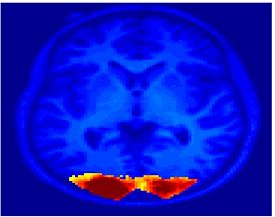
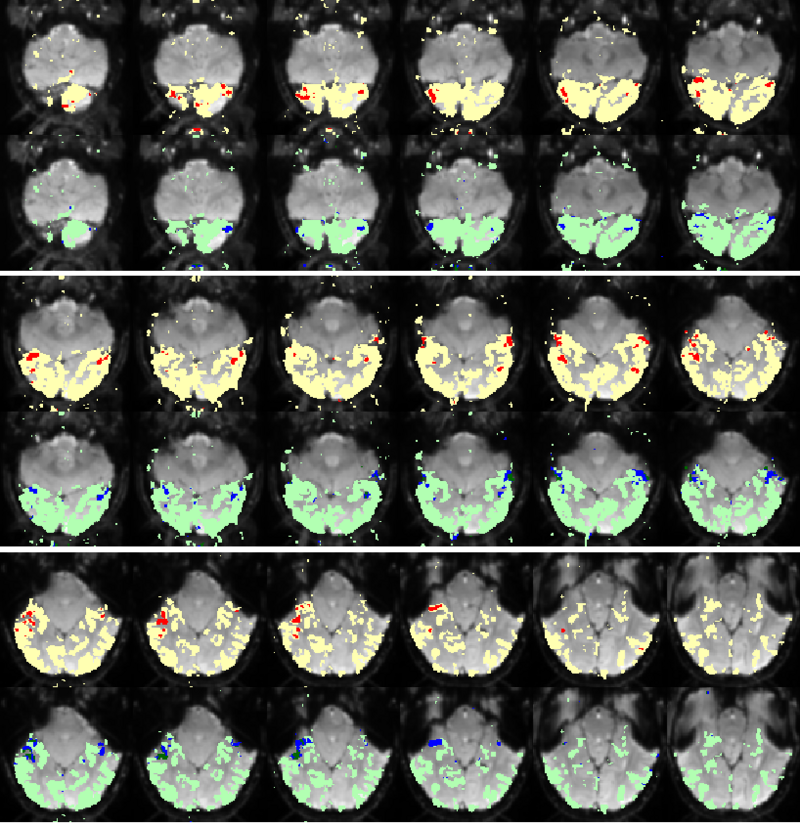
Fig.3 presents the group average of the subject-specific 2-system maps. Color shading shows the proportion of subjects whose clustering agreed with the majority label. Fig. 4 shows the group average of a further parcelation of the intrinsic system, i.e., one of two clusters associated with the non-stimulus-driven regions. In order to present a validation of the method, we compare these results with the conventional scheme for detection of visually responsive areas. In Fig. 5, color shows the statistical parametric map while solid lines indicate the boundaries of the visual system obtained through clustering. The result illustrate the agreement between the two methods.

Fig 3. 2-System Parcellation. Group-wise result.	Fig 4. Validation: Parcelation of the intrinsic system.

Fig 5. Validation: Visual system.

Exploring Functional Connectivity in fMRI via Clustering

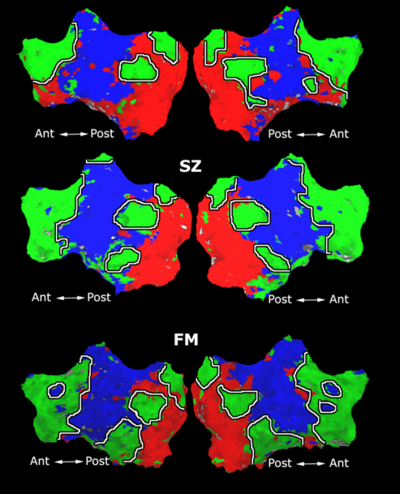
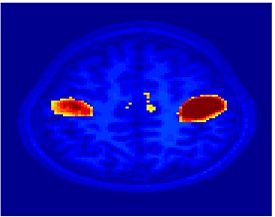
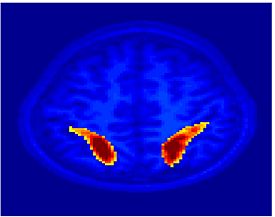
As a continuation to the above experiments, we apply two distinct clustering algorithms to functional connectivity analysis: K-Means clustering and Spectral Clustering. The K-Means algorithm assumes that each voxel time course is drawn independently from one of k multivariate Gaussian distributions with unique means and spherical covariances. In contrast, Spectral Clustering does not presume any parametric form for the data. Rather it captures the underlying signal geometry by inducing a low-dimensional representation based on a pairwise affinity matrix constructed from the data. Without placing any a priori constraints, both clustering methods yield partitions that are associated with brain systems traditionally identified via seed-based correlation analysis. Our empirical results suggest that clustering provides a valuable tool for functional connectivity analysis.

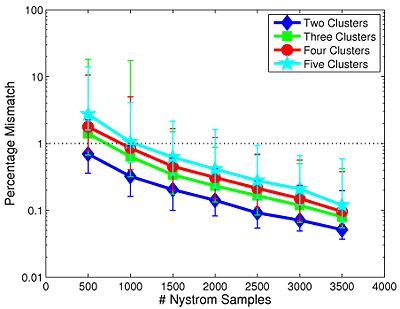
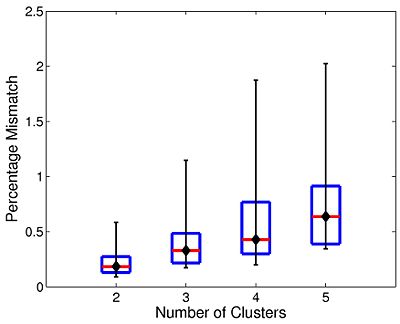
One downside of Spectral Clustering is that it relies on the eigen-decomposition of an NxN affinity matrix, where N is the number of voxels in the whole brain. Since N is on the order of ~200,000 voxels, it is infeasible to compute the full eigen-decomposition given realistic memory and time constraints. To solve this problem, we approximate the leading eigenvalues and eigenvectors of the affinity matrix via the Nystrom Method. Empirically, we find that the Nystrom Method produces consistent partitions of the brain across different random initializations.

We validate these algorithms on resting state data collected from 45 healthy young adults (mean age 21.5, 26 female). Four 2mm isotropic functional runs were acquired from each subject. Each scan lasted for 6m20s with TR = 5s. The first 4 time points in each run were discarded, yielding 72 time samples per run. The entire brain volume is partitioned into an increasing number of clusters. We perform standard preprocessing on each of the four runs, including motion correction by rigid body alignment of the volumes, slice timing correction and registration to the MNI atlas space. The data is spatially smoothed with a 6mm 3D Gaussian filter, temporally low-pass filtered using a 0.08Hz cutoff, and motion corrected via linear regression. Next, we estimate and remove contributions from the white matter, ventricle and whole brain regions (assuming a linear signal model). We mask the data to include only brain voxels and normalized the time courses to have zero mean and unit variance. Finally, we concatenate the four runs into a single time course for analysis.

Fig 1. Median clustering difference when varying the number of Nystrom Samples	Fig 2. Nystrom clustering consistency using random 2,000 samples per trial.

Spectral Clustering (SC)	K-Means (KM)	Seed-Based (SBA)
Spectral Clustering	K-Means	Seed-Based

Clustering Study of Domain Specificity in High Level Visual Cortex

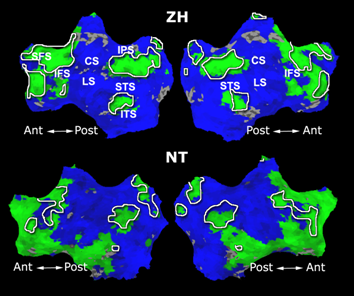
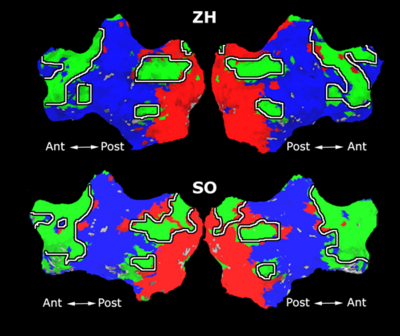
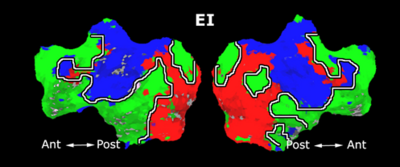
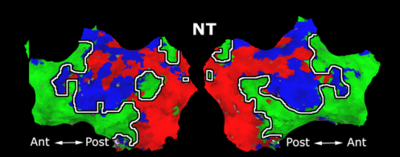
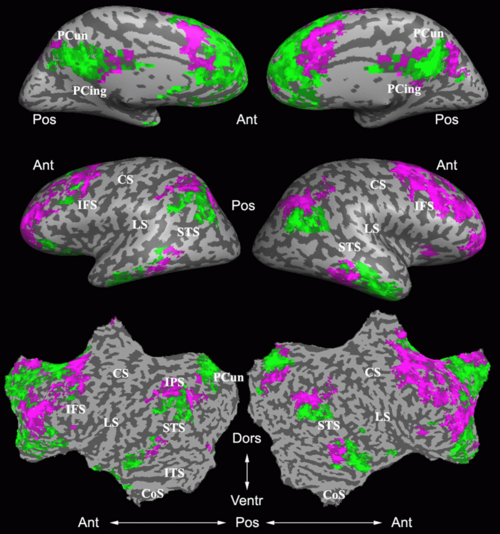
As a more specific application of model-based clustering algorithms, we are devising clustering algorithms for detection of functional connectivity in high-level visual cortex. It is suggested that there are regions in the visual cortex with high selectivity to certain categories of visual stimuli. Currently, the conventional method for detection of these methods is based on statistical tests comparing response of each voxel in the brain to different visual categories to see if it shows considerably higher activation to one category. For example, the well-known FFA (Fusiform Face Area) is the set of voxels which show high activation to face images. We use a model-based clustering approach to the analysis of this type of data as a means to make this analysis automatic and further discover new structures in the high-level visual cortex.

Introducing the notion of space of activation profiles, we construct a representation of the data which explicitly parametrizes all interesting patterns of activation. Mapping the data into this space, we formulate a model-based clustering algorithm that simultaneously finds a set of activation profiles and their spatial maps. We validate our method on the data from studies of category selectivity in visual cortex, demonstrating good agreement with the findings based on prior hypothesis-driven methods. This model enables functional group analysis independent of spatial correspondence among subjects. We are currently working on a co-clustering extension of this algorithm which can simultaneously find a set of clusters of voxels and meta-categories of stimuli in experiments with diverse sets of stimulus categories.

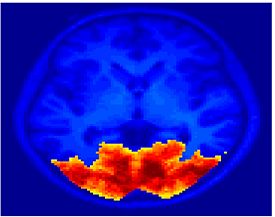
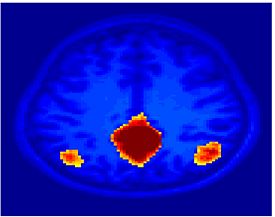
Fig. 6 compares the map of voxels assigned to a face-selective profile by our algorithm with the t-test's map of voxels with statistically significant (p<0.0001) response to faces when compared with object stimuli. Note that in contrast with the hypothesis testing method, we don't specify the existence of a face-selective region in our algorithm and the algorithm automatically discovers such a profile of activation in the data.

Fig 6. Spatial maps of the face selective regions found by the statistical test (red) and our mixture model (dark blue). Maps are presented in alternating rows for comparison. Visually responsive mask of voxels used in our experiment is illustrated in yellow and light blue.

Comparison of Data-Driven Analysis Methods for Identification of Functional Connectivity in fMRI

Although ICA and clustering rely on very different assumptions on the underlying distributions, they produce surprisingly similar results for signals with large variation. Our main goal is to evaluate and compare the performance of ICA and clustering based on Gaussian mixture model (GMM) for identification of functional connectivity. Using the synthetic data with artificial activations and artifacts under various levels of length of the time course and signal-to-noise ratio of the data, we compare both spatial maps and their associated time courses estimated by ICA and GMM to each other and to the ground truth. We choose the number of sources via the model selection scheme, and compare all of the resulting components of GMM and ICA, not just the task-related components, after we match them component-wise using the Hungarian algorithm. This comparison scheme is verified in a high level visual cortex fMRI study. We find that ICA requires a smaller number of total components to extract the task-related components, but also needs a large number of total components to describe the entire data. We are currently applying ICA and clustering methods to connectivity analysis of schizophrenia patients.

Key Investigators

• MIT Algorithms: Danial Lashkari, Y. Bryce Kim, Archana Venkataraman, Polina Golland, Nancy Kanwisher.
• Harvard DBP 2: J. Oh, Marek Kubicki.

Publications

In print

• NA-MIC Publications Database

In press