Difference between revisions of "Projects:NonParametricClustering"
| Line 16: | Line 16: | ||
|} | |} | ||
| − | + | == Clustering method == | |
| + | Our method of choice for the clustering of the data space is based on a physical Potts model. The N points of our dataset are referred as magnetic sites. Each site is assigned a Potts spin. Spin values are taken from a set of q distinct integers. An interaction term that is proportional to the distance between nearest neighbor’s data points is added to the model. The spin configuration of our model is dependent on a parameter T that physically corresponds to a temperature. Such Potts systems are known to form a phase with islands of similar Potts state (similar magnetic state). Revealing the clusters in the data space is converted into Monte Carlo search for the magnetic islands in the equivalent physical model. While this method is slow comparing to other non parametric hierarchical methods, it is by far superior in robustness and its classification is more coherent due to its physical interpretation. We compare our results to linkage-based clustering methods, which are popular non-parametric clustering methods. | ||
| + | |||
| + | |||
| + | == Results == | ||
| + | |||
| + | === Single Nucleotide === | ||
| + | |||
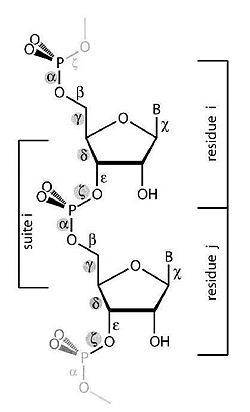
| + | The single nucleotide conformation is the basic structural unit of the RNA shape. The flexibility of a residue stems from the modes of motion of its backbone, which are restricted to 6 rotations. The backbone conformation distribution is strongly non-homogeneous and we then operate clustering in this 6-dimensional torsional space. | ||
| + | |||
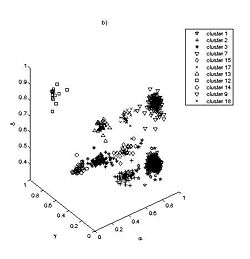
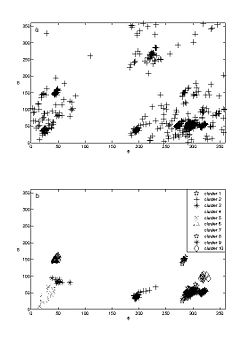
| + | Comparison of the resulting clustering with previous prior knowledge reveals an excellent match (Fig 2). | ||
| + | |||
{| | {| | ||
|+ '''Fig 2. Single Nucleotide Representations''' | |+ '''Fig 2. Single Nucleotide Representations''' | ||
Revision as of 22:27, 9 December 2008
Home < Projects:NonParametricClusteringBack to NA-MIC Collaborations, Georgia Tech Algorithms
Non Parametric Clustering for Biomolecular Structural Analysis
High accuracy imaging and image processing techniques allow for collecting structural information of biomolecules with atomistic accuracy. Direct interpretation of the dynamics and the functionality of these structures with physical models, is yet to be developed. Clustering of molecular conformations into classes seems to be the first stage in recovering the formation and the functionality of these molecules. The lack of prior knowledge such as number and shape of the clusters in the data space can be resolved most efficiently by using non parametric clustering methods. We are currently developing an application based on a Potts model method that was proposed by Blatt Wiseman and Domany to deal with the structure of the biomolecules.
Description
The purpose of this work is to adapt a non-parametric clustering algorithm for data mining of RNA structures. One of the main challenges of bioinformatics is to develop data mining tools for the available RNA structures from data banks in order to establish structure-function relationship. To do so a coherent objective classification method is required. To test such methods we are currently analyzing the conformational data space of single and double nucleotides only (Fig 1).
Clustering method
Our method of choice for the clustering of the data space is based on a physical Potts model. The N points of our dataset are referred as magnetic sites. Each site is assigned a Potts spin. Spin values are taken from a set of q distinct integers. An interaction term that is proportional to the distance between nearest neighbor’s data points is added to the model. The spin configuration of our model is dependent on a parameter T that physically corresponds to a temperature. Such Potts systems are known to form a phase with islands of similar Potts state (similar magnetic state). Revealing the clusters in the data space is converted into Monte Carlo search for the magnetic islands in the equivalent physical model. While this method is slow comparing to other non parametric hierarchical methods, it is by far superior in robustness and its classification is more coherent due to its physical interpretation. We compare our results to linkage-based clustering methods, which are popular non-parametric clustering methods.
Results
Single Nucleotide
The single nucleotide conformation is the basic structural unit of the RNA shape. The flexibility of a residue stems from the modes of motion of its backbone, which are restricted to 6 rotations. The backbone conformation distribution is strongly non-homogeneous and we then operate clustering in this 6-dimensional torsional space.
Comparison of the resulting clustering with previous prior knowledge reveals an excellent match (Fig 2).
Project status
Thus far we have applied the method to classify single nucleotide conformation. Comparison of the resulting clustering with previous prior knowledge based K mean algorithm reveals an excellent match (Fig 2). We have also reconstructed with high fidelity the consensus base pair classification (Fig 3). At the current stage we are developing classification nomenclature for base stacking, an interaction that have not been given an adequate physical model nor been classified.
Project aim
A variant of the Potts model classification can be used to find clustering in network of interactions between molecules. We plan to use the Potts model with results from projects of polymers adsorption that we are currently working on to develop model for docking interactions between polymers and of polymer with surfaces.
Key Investigators
- Georgia Tech: E. Hershkovits, X. Le Faucheur, R. Tannenbaum and A. Tannenbaum
Publications
In Print
In press
- X. Le Faucheur, E. Hershkovits, R. Tannenbaum and A. Tannenbaum. Non-Parametric Clustering for studying RNA conformation. Publication in submission.