Difference between revisions of "Projects:LearningRegistrationCostFunctions"
| Line 32: | Line 32: | ||
== (1) Localizing Brodmann Areas Using Cortical Folding == | == (1) Localizing Brodmann Areas Using Cortical Folding == | ||
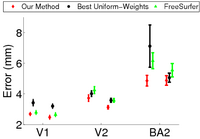
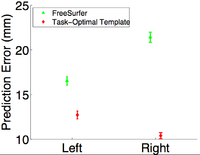
| − | In this experiment, we estimate the optimal template in the wSSD cost function for localizing Brodmann areas in 10 histologically-analyzed subjects. We compare 3 algorithms: task-optimal template (red), FreeSurfer (green) [1] and optimal uniform weights (black). Optimal uniform weights are found by setting all the weights to a single value and performing an exhaustive search of the weights. | + | In this experiment, we estimate the optimal template in the wSSD cost function for localizing Brodmann areas in 10 histologically-analyzed subjects. We compare 3 algorithms: task-optimal template (red), FreeSurfer (green) [1] and optimal uniform weights (black). Optimal uniform weights are found by setting all the weights to a single value and performing an exhaustive search of the weights. We see in the figure below, that task-optimal framework achieves the lowest localization errors. |
<center> | <center> | ||
| Line 48: | Line 48: | ||
== (2) Localizing fMRI-defined MT+ Using Cortical Folding == | == (2) Localizing fMRI-defined MT+ Using Cortical Folding == | ||
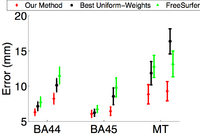
| + | In this experiment, we consider 42 subjects with fMRI-defined MT+ defined on the subject. MT+ is thought to include the cytoarchitectonically-defined MT, as well as, a small part of the medial superior temporal region. | ||
| + | |||
| + | [[Image:exvivoMTPredictsInvivoMT.png|thumb|center|200px]] | ||
| + | |||
Revision as of 19:24, 10 September 2009
Home < Projects:LearningRegistrationCostFunctionsBack to NA-MIC Collaborations, MIT Algorithms
We present a framework for learning registration cost functions. In medical image analysis, registration is rarely the final goal, but instead the resulting alignment is used in other tasks, such as image segmentation or group analysis. The parameters of the registration cost function -- for example, the tradeoff between the image similarity and regularization terms -- are typically determined manually through inspection of the image alignment and then fixed for all applications. However, it is unclear that the same parameters are optimal for different applications. In this work, we propose a principled approach to leveraging the application context to effectively regularize the ill-posed problem of image registration. Our method learns the parameters of any smooth family of registration cost functions with respect to a specific task.
Contents
Motivation
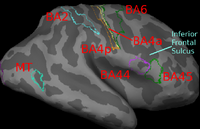
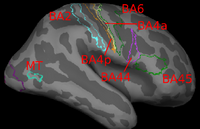
Image registration is ambiguous. For example, Brodmann areas are parcellation of the cortex based on the cellular architecture of the cortex. The figures below show two subjects with Brodmann areas overlaid on the cortical folding pattern. Here, we see that perfectly aligning the inferior frontal sulcus will misalign the superior end of BA44 (Broca's language area). If our goal is segment sulci and gyri, perfectly alignment of the cortical folding pattern is ideal. But it is unclear whether perfectly aligning cortical folds is optimal for localizing Brodmann areas. Here, we show that by taking into account the end-goal of registration, we not only improve the application performance but also potentially eliminate ambiguities in image registration.
Description
The key idea is to introduce a second layer of optimization over and above the usual registration. This second layer of optimization traverses the space of local minima, selecting registration parameters that result in good registration local minima as measured by the performance of the specific application in a training data set. The training data provides additional information not present in a test image, allowing the task-specific cost function to be evaluated during training. For example, if the task is segmentation, we assume the existence of a training data set with ground truth segmentation and a smooth cost function that evaluates segmentation accuracy. This segmentation accuracy is used as a proxy to evaluate registration accuracy.
If the registration cost function employs a single parameter, then the optimal parameter value can be found by exhaustive search. With multiple parameters, exhaustive search is not possible. Here, we demonstrate the optimization of thousands of parameters by gradient descent on the space of local minima, selecting registration parameters that result in good registration local minima as measured by the task-specific cost function in the training data set.
Our formulation is related to the use of continuation methods in computing the entire path of solutions of learning problems (e.g., SVM or Lasso) as a function of a single regularization parameter. Because we deal with multiple (thousands of) parameters, it is impossible for us to compute a solution manifold. Instead, we trace a path within the solution manifold that improves the task-specific cost function.
Another advantage of our approach is that we do not require ground truth deformations. As suggested in the example above, the concept of “ground truth deformations” may not always be well-defined, since the optimal registration may depend on the application at hand. In contrast, our approach avoids the need for ground truth deformations by focusing on the application performance, where ground truth (e.g., via segmentation labels) is better defined.
Experimental Results
We instantiate the framework for the alignment of hidden labels whose extents are not necessarily well-predicted by local image features. We consider the generic weighted Sum of Squared Differences (wSSD) cost function and estimate either (1) the optimal weights or (2) cortical folding template for localizing cytoarchitectural and functional regions based only on macroanatomical cortical folding information. We demonstrate state-of-the-art localization results in both histological and fMRI data sets.
(1) Localizing Brodmann Areas Using Cortical Folding
In this experiment, we estimate the optimal template in the wSSD cost function for localizing Brodmann areas in 10 histologically-analyzed subjects. We compare 3 algorithms: task-optimal template (red), FreeSurfer (green) [1] and optimal uniform weights (black). Optimal uniform weights are found by setting all the weights to a single value and performing an exhaustive search of the weights. We see in the figure below, that task-optimal framework achieves the lowest localization errors.
(2) Localizing fMRI-defined MT+ Using Cortical Folding
In this experiment, we consider 42 subjects with fMRI-defined MT+ defined on the subject. MT+ is thought to include the cytoarchitectonically-defined MT, as well as, a small part of the medial superior temporal region.
[1] B. Fischl, M. Sereno, R. Tootell, and A. Dale. High-resolution Intersubject Averaging and a Coordinate System for the Cortical Surface. Human Brain Mapping, 8(4):272–284, 1999.
Key Investigators
- MIT: [| B.T. Thomas Yeo], Mert Sabuncu, Polina Golland
- MGH: Bruce Fischl, Daphne Holt
- INRIA: Tom Vercauteren
- Aachen University: Katrin Amunts
- Research Center Juelich: Karl Zilles
Publications
In Print