Difference between revisions of "Projects:BrainManifold"
From NAMIC Wiki
m (Stub) |
|||
| Line 2: | Line 2: | ||
__NOTOC__ | __NOTOC__ | ||
= Brain Manifold Learning = | = Brain Manifold Learning = | ||
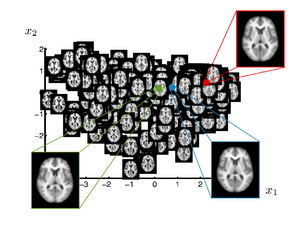
| + | [[Image:sgerber_brainmanifold_oasis_manifold.png|thumb|300px|Manifold learned from OASIS database. The image shows a 2-dimensional parametrization of the database. The green, red and blue are the mean, median and mode images computed using the manifold representation]] | ||
| − | + | This work investigates the use of manifold learning approaches in the context of brain population analysis. The goal is to construct a manifold model from a set of brain images that captures variability in shape, a parametrization of the shape space. | |
| − | + | Such a manifold model is interesting in several ways | |
| − | + | * The low dimensional parametrization simplifies statistical analysis of populations. | |
| − | + | * Applications to searching and browsing large database | |
| − | + | * The manifold represents a localized Atlas. Alternative to template based applications. For example as a segmentation prior. | |
| − | + | * Aid in clinical diagnosis. Different regions on the manifold can indicate different pathologies. | |
= Description = | = Description = | ||
| Line 19: | Line 20: | ||
= Publications = | = Publications = | ||
| + | = Publications = | ||
| + | |||
| + | |||
| + | ''Published in MICCAI and ICCV'' | ||
| + | * [http://www.cs.utah.edu/~sgerber/research/ Manifold Learning Research Page] | ||
| + | * [http://www.na-mic.org/publications/pages/display?search=BrainManifold&submit=Search&words=all&title=checked&keywords=checked&authors=checked&abstract=checked&sponsors=checked&searchbytag=checked| NA-MIC Publications Database] | ||
| − | + | [[Category:Statistics]] [[Category:Registration]] | |
Revision as of 18:35, 7 October 2009
Home < Projects:BrainManifoldBack to Utah Algorithms
Brain Manifold Learning
This work investigates the use of manifold learning approaches in the context of brain population analysis. The goal is to construct a manifold model from a set of brain images that captures variability in shape, a parametrization of the shape space. Such a manifold model is interesting in several ways
- The low dimensional parametrization simplifies statistical analysis of populations.
- Applications to searching and browsing large database
- The manifold represents a localized Atlas. Alternative to template based applications. For example as a segmentation prior.
- Aid in clinical diagnosis. Different regions on the manifold can indicate different pathologies.
Description
Key Investigators
- Utah: Samuel Gerber, Tolga Tasdizen, Sarang Joshi, Tom Fletcher, Ross Whitaker
Publications
Publications
Published in MICCAI and ICCV