Difference between revisions of "Projects:Utah2ShapeRegression"
| Line 14: | Line 14: | ||
= Results = | = Results = | ||
| − | + | {| border="0" style="background:transparent;" | |
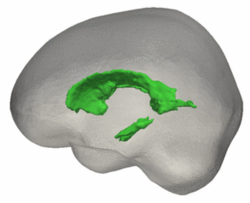
| + | |[[File:VentShape-Regression.PNG|250px|center|thumb|Brain ventricle change from 4 to 8 years.]] | ||
| + | |[[File:VentShape-Regression-2.PNG|250px|center|thumb|Shape regression: First time point]] | ||
| + | |[[File:VentShape-Regression-3.PNG|250px|center|thumb|Shape regression: Last time point]] | ||
| + | |- | ||
| + | |} | ||
= Literature = | = Literature = | ||
Revision as of 04:11, 12 April 2011
Home < Projects:Utah2ShapeRegressionBack to Utah 2 Algorithms
Smooth Growth Trajectories from Time Series Shape Data
Segmentation of multi-time point image data of individual subjects results in serial shape data of structures of interest. Clinical research is interested in the spatiotemporal analysis of shape changes, which potentially leads to improved understanding of the rate of change, locality and growth trajectory of structures of interest.
Description
Longitudinal shape analysis often relies on the estimation of a realistic continuous growth scenario from data sparsely distributed in time. In this project, we develop a new type of growth model parameterized by acceleration, whereas standard methods usually control the velocity [1,2]. From this parameterization, we gain one order of differentiability and guarantee that shape evolution is smooth in both space and time. This mimics the behavior of biological tissue as a mechanical system driven by external forces. The growth trajectories are estimated as continuous flows of deformations, which are twice differentiable. In pilot tests on an infant growth study, we demonstrate that volume measurements taken out of our 3D shape regression are compatible with a 1D regression of these measurements. This implies that also other morphometric measurements of interest for clinicians might be smooth and thus model biological change in a realistic way. Leave-several-out experiments demonstrate that the new method better interpolates between data and is therefore more robust to missing observations. This suggests a greater ability to capture the underlying growth of the anatomical structures.
Results
Literature
[1] Miller, M, I., Trouve, A., Younes, L.: On the metrics and Euler-Lagrange equations of Computational Anatomy. Annual Review of Biomedical Engineering 4 (2002), 375–405
[2] Durrleman, S., Pennec, X., Trouve, A., Gerig, G., Ayache, N.: Spatiotemporal atlas estimation for developmental delay detection in longitudinal datasets. In: Proc. of MICCAI’09, Part I. (2009) 297–304
Key Investigators
- Utah: James Fishbaugh, Stanley Durrleman, Guido Gerig
- IOWA: Hans Johnson