Difference between revisions of "Projects:LongitudinalShapeAnalysis"
Jfishbaugh (talk | contribs) |
Jfishbaugh (talk | contribs) |
||
| Line 13: | Line 13: | ||
== Description == | == Description == | ||
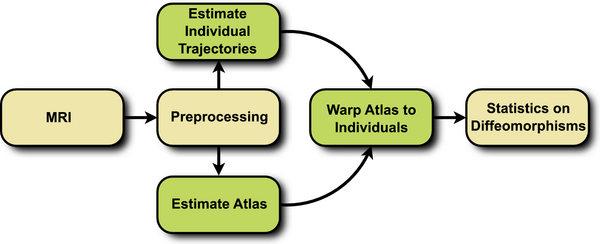
| − | The proposed framework consists of three steps, summarized in Fig. 1. First, a cross-sectional atlas is estimated by shape regression, which can be thought of Fig. 1. Flowchart depicting the proposed method. as normative, reference evolution. Second, subject specific growth trajectories are estimated independently for each individual, accounting for intra-subject variability. Third, a homologous space for statistical analysis is obtained by warping the atlas to each individual at any time point of interest | + | The proposed framework consists of three steps, summarized in Fig. 1. First, a cross-sectional atlas is estimated by shape regression, which can be thought of Fig. 1. Flowchart depicting the proposed method. as normative, reference evolution. Second, subject specific growth trajectories are estimated independently for each individual, accounting for intra-subject variability. Third, a homologous space for statistical analysis is obtained by warping the atlas to each individual at any time point of interest. |
[[File:Flowchart_long_shapes.png|600px|center|thumb|'''Fig. 1.''' Flowchart depicting the proposed method.]] | [[File:Flowchart_long_shapes.png|600px|center|thumb|'''Fig. 1.''' Flowchart depicting the proposed method.]] | ||
| + | |||
| + | The first two steps require the estimation of a growth model, the specifics of which are discussed in the next section. Here we use the acceleration controlled growth model of [1], where shape evolution is modeled as a continuous flow of deformation. A baseline shape is continuously deformed over time to match the target shapes. The estimation is posed as a variational problem balancing fidelity to data with regularity. The parameterization by acceleration guarantees that the estimated evolution is temporally smooth. Furthermore, the acceleration controlled growth model is generic, with no constraint that the flow of deformation must follow a | ||
| + | geodesic path, or close to a geodesic path. | ||
| + | |||
| + | For measuring shape similarity, we use the metric on currents [2]. This way, shapes are modeled as distributions, alleviating the need for explicit point correspondence between shapes. | ||
== Results == | == Results == | ||
Revision as of 21:02, 14 August 2012
Home < Projects:LongitudinalShapeAnalysisBack to Utah 2 Algorithms
Ongoing Work (Updated 8/14/12)
Analysis of Longitudinal Shape Variability
Quantification of anatomical variability within a population and between populations are fundamental tasks in medical imaging studies. In many clinical applications, it is particularly crucial to quantify anatomical variability over time in order to determine disease progression and to isolate clinically important differences in both space and time. Such studies are designed around longitudinal imaging, where we acquire repeated measurements over time of the same subject, which yields rich data for analysis. Statistical analysis of longitudinal anatomical data is a problem with significant challenges due to the difficulty in modeling anatomical changes, such as growth, and comparing changes across different populations.
In this project, we propose a new approach for analyzing statistical variability of shapes over time, in the spirit of which is based on combining cross-sectional atlas construction with subject specific growth modeling. The growth model used for shape regression naturally handles multiple shapes at each time point and does not require point correspondence between subjects, making the proposed framework both convenient and applicable to a wide range of clinical problems.
Description
The proposed framework consists of three steps, summarized in Fig. 1. First, a cross-sectional atlas is estimated by shape regression, which can be thought of Fig. 1. Flowchart depicting the proposed method. as normative, reference evolution. Second, subject specific growth trajectories are estimated independently for each individual, accounting for intra-subject variability. Third, a homologous space for statistical analysis is obtained by warping the atlas to each individual at any time point of interest.
The first two steps require the estimation of a growth model, the specifics of which are discussed in the next section. Here we use the acceleration controlled growth model of [1], where shape evolution is modeled as a continuous flow of deformation. A baseline shape is continuously deformed over time to match the target shapes. The estimation is posed as a variational problem balancing fidelity to data with regularity. The parameterization by acceleration guarantees that the estimated evolution is temporally smooth. Furthermore, the acceleration controlled growth model is generic, with no constraint that the flow of deformation must follow a geodesic path, or close to a geodesic path.
For measuring shape similarity, we use the metric on currents [2]. This way, shapes are modeled as distributions, alleviating the need for explicit point correspondence between shapes.
Results
Key Investigators
- Utah: James Fishbaugh, Marcel Prastawa, Guido Gerig
- INRIA/ICM, Pitie Salpetriere Hospital: Stanley Durrleman
- Carolina Institute for Developmental Disabilities: Joseph Piven