Projects:NonRegularSurfCorres

Back to Utah Algorithms

Geometric Correspondence for Nonregular Surfaces

Examples of challenges posed by nonregular surfaces.

Description

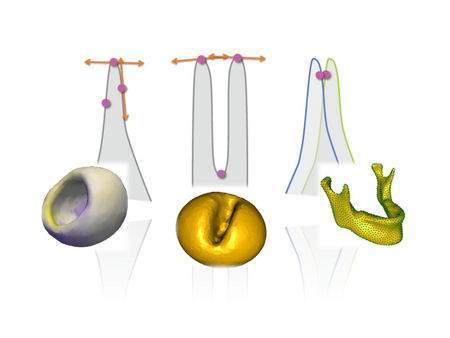
An ensemble of biological shapes can be represented and analyzed with a dense set of point correspondences. In previous work, optimal point placement was determined by optimizing an information theoretic criterion that depends on relative spatial locations on different shapes combined with pairwise Euclidean distances between nearby points on the same shape. These choices have prevented such methods from effectively characterizing shapes with complex geometry such as thin or highly curved features. This paper extends previous methods for automatic shape correspondence by taking into account the underlying geometry of individual shapes. This is done by replacing the Euclidean distance for intrashape pairwise particle interactions by the geodesic distance. A novel set of numerical techniques for fast distance computations on curved surfaces is used to extract these distances. In addition, we introduce an entropy term that incorporates surface normal information to achieve better particle correspondences near sharp features. Finally, we demonstrate this new method on synthetic and biological datasets.

Key Investigators

• Utah: Manasi Datar, Yaniv Gur, Ross Whitaker
• UNC: Beatriz Paniagua, Martin Styner

Publications

• M Datar, Y Gur, B Paniagua, M Styner, R Whitaker, | Geometric Correspondence for Ensembles of Nonregular Shapes, MICCAI 2011