NA-MIC/Projects/fMRI Analysis/Conformal Flattening for fMRI Visualization

Back to NA-MIC_Collaborations

Objective: We want to develop new flattening methods for better visualizing neural activity from fMRI brain imagery. Our technique is based on conformal mappings which map the cortical surface onto a sphere in an angle preserving manner.

Introduction We have worked on several techniques for flattening brain surfaces for visualization. Brain flattening has a number of uses including in functional magnetic resonance imaging data in order to better visualize neural activity within the three dimensional folds of the cortex.

The basic idea is that the grey cortical matter surface is the same as that of a crumpled sheet, and in particular does not have any holes or self-intersections. Our approach to flattening such a surface is based on a well-known technique in the theory of Riemann surfaces from complex analysis and geometry, namely, that a surface of genus zero (no handles) without any holes or self-interesections can be mapped conformally onto the sphere, and any local portion thereof onto a disc. In this way, the brain surface may be flattened. The mapping is conformal in the sense that angles are preserved. Moreover, one can explicitly write down how the metric is transformed and thus the geodesics as well. Hence the flattening mapping can be used to obtain an atlas of the brain surface in a straightforward, canonical manner.

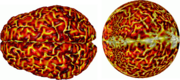
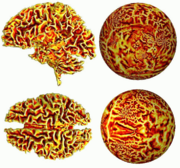
The key observation is that the flattening function may be obtained as the solution of a second order elliptic equation on the surface to be flattened. For triangulated surfaces, there exist powerful reliable finite element procedures which can be employed to numerically approximate the flattening function. Some examples of flattened surfaces are given below in Figures 1 and 2.

Progress: We have developed code for conformal flattening which has been incorporated into Slicer.

Surface flattening is a technique that associates a coordinate in the image with each location on the surface of a geometric object. This technology can be used on a vessel surface, brain surface, or colon surface, just to list a few medical examples.

Figure 1: Flattening of the Cortical Surface

Figure 2: Flattening of White/Gray Matter Surface

(From S. Angenent, S. Haker, A. Tannenbaum, and R. Kikinis, “On the Laplace-Beltrami operator and brain surface flattening,” IEEE Trans. on Medical Imaging, Vol. 18, pp. 700-711, 1999.)

Key Investigators:

• GATech: Yi Gao, John Melonakos, Shawn Lankton, Allen Tannenbaum
• Harvard: Steven Haker, Ron Kikinis

Links:

• Stony Brook Page