Difference between revisions of "Projects:KPCA LLE KLLE ShapeAnalysis"
| Line 3: | Line 3: | ||
kernel locally linear embedding (KLLE). | kernel locally linear embedding (KLLE). | ||
| − | + | == Shape Representation == | |
The surfaces are represented as the zero level set of a signed distance function and shape learning is performed on the embeddings of these shapes. We carry out some experiments to see how well each of these methods can represent a shape, given the training set. We tested the performance of these methods on shapes of left caudate nucleus and left hippocampus. The training set of left caudate nucleus consisted of 26 data sets and the test set contained 3 volumes. Error between a particular shape representation and | The surfaces are represented as the zero level set of a signed distance function and shape learning is performed on the embeddings of these shapes. We carry out some experiments to see how well each of these methods can represent a shape, given the training set. We tested the performance of these methods on shapes of left caudate nucleus and left hippocampus. The training set of left caudate nucleus consisted of 26 data sets and the test set contained 3 volumes. Error between a particular shape representation and | ||
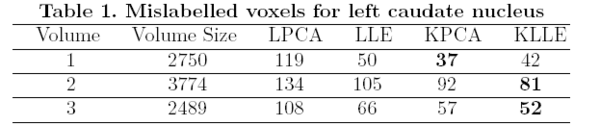
ground truth was calculated by computing the number of mislabeled voxels using each of the methods. Figure 1 gives the error | ground truth was calculated by computing the number of mislabeled voxels using each of the methods. Figure 1 gives the error | ||
Revision as of 16:27, 2 April 2007
Home < Projects:KPCA LLE KLLE ShapeAnalysisObjective
To compare various shape representation techniques like linear PCA (LPCA), kernel PCA (KPCA), locally linear embedding (LLE) and kernel locally linear embedding (KLLE).
Shape Representation
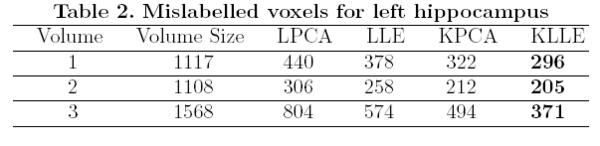
The surfaces are represented as the zero level set of a signed distance function and shape learning is performed on the embeddings of these shapes. We carry out some experiments to see how well each of these methods can represent a shape, given the training set. We tested the performance of these methods on shapes of left caudate nucleus and left hippocampus. The training set of left caudate nucleus consisted of 26 data sets and the test set contained 3 volumes. Error between a particular shape representation and ground truth was calculated by computing the number of mislabeled voxels using each of the methods. Figure 1 gives the error using each of the methods. Similar tests were done on a training set of 20 hippocampus data with 3 test volumes. Figure 2 gives the error table for each of the methods [1].
References
- [1] Y. Rathi, S. Dambreville, and A. Tannenbaum. "Comparative Analysis of Kernel Methods for Statistical Shape Learning", In CVAMIA held in conjunction with ECCV, 2006.
Key Investigators
- Core 1:
- Georgia Tech: Yogesh Rathi, Samuel Dambreville, Allen Tannenbaum
Links:
- Paper presented in CVAMIA2006 in conjunction with ECCV 2006
- Georgia Tech Summary Page
- NA-MIC_Collaborations