Difference between revisions of "Algorithm:Utah"
| Line 74: | Line 74: | ||
a point-based sampling of the shape ensemble that simultaneously maximizes | a point-based sampling of the shape ensemble that simultaneously maximizes | ||
both the geometric accuracy and the statistical simplicity of the | both the geometric accuracy and the statistical simplicity of the | ||
| − | model. Surface point samples, which also define the shape-to-shape correspondences, | + | model. Surface point samples, which also define the shape-to-shape correspondences, are modeled as sets of dynamic particles that are constrained |
| − | are modeled as sets of dynamic particles that are constrained | ||
to lie on a set of implicit surfaces. Sample positions are optimized by gradient | to lie on a set of implicit surfaces. Sample positions are optimized by gradient | ||
descent on an energy function that balances the negative entropy | descent on an energy function that balances the negative entropy | ||
| Line 81: | Line 80: | ||
of shapes. We also extend the method with a curvature-adaptive | of shapes. We also extend the method with a curvature-adaptive | ||
sampling strategy in order to better approximate the geometry of the | sampling strategy in order to better approximate the geometry of the | ||
| − | objects. We have developed code based on ITK for computation of correspondence-based | + | objects. We have developed code based on ITK for computation of correspondence-based models, and have validated out method in several papers against several synthetic and real examples in two and three dimensions, including application to the statistical shape analysis of brain structures. We used hippocampus data from a schizo-typal personality disorder (SPD) study funded by |
| − | models, and have validated out method in several papers against several synthetic and real | + | the Stanley Foundation and UNC-MHNCRC (MH33127), and caudate data from a schizophrenia |
| − | examples in two and three dimensions, including application to the statistical | + | study funded by NIMH R01 MH 50740 (Shenton), NIH K05 MH 01110 (Shenton), NIMH |
| − | shape analysis of brain structures. Our most recent work is in the application of the | + | R01 MH 52807 (McCarley), and a VA Merit Award (Shenton). |
| − | particle method to | + | |
| + | Figure 1,2 illustrates results of hypothesis testing for group differences from the control population for the left/right hippocampus and the left/right caudate. Raw and FDR-corrected p-values are given. Areas of significant | ||
| + | group differences ($p <= 0.05$) are shown as dark regions. Areas with insignificant | ||
| + | group differences ($p > 0.05$) are shown as light regions. Our results correlate with with other published hypothesis testing results on this data. | ||
| + | |||
| + | Our most recent work is in the application of the particle method to multi-object shape complexes. We have developed a novel method for computing surface point correspondences of multi-object anatomy that | ||
| + | is a straightforward extension of the particle method for single-object anatomy. The correspondences take advantage of the statistical structure of an ensemble of complexes, and thus they are suitable for joint statistical analyses of shape and relative pose. The proposed method uses a dynamic particle system to optimize correspondence point positions across all structures in a complex | ||
| + | simultaneously, in order to create a compact model of ensemble statistics. | ||
| + | It is a different approach from previous methods for dealing with shape | ||
| + | complexes, because to date researchers have considered the correspondence | ||
| + | problem only for each structure independently, and have ignored intermodel | ||
| + | correlations in the shape parameterization. These correlations are | ||
| + | particularly important when the correspondences are constructed in order to | ||
| + | reduce or minimize the information content of the ensemble. | ||
| + | |||
| + | [[Image:Lcomb-grayscale.png|thumbnail|Figure 1]] | ||
| + | [[Image:Rcomb-grayscale.png|thumbnail|Figure 2]] | ||
| + | |||
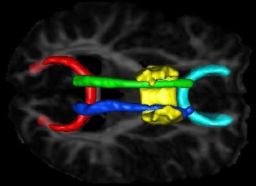
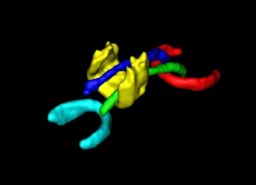
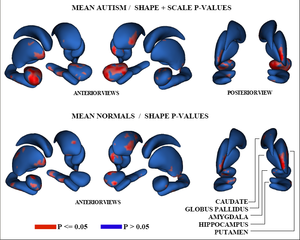
| + | We have developed a formulation of the multi-object correspondence optimization, and have applied it to a proof-of-concept application to the analysis of brain structure complexes from a longitudinal study of pediatric autism that is underway at UNC chapel hill. This work is in conjunction with Martin Styner, Heather Cody Hazlett, and Joe Piven. Figure 3 shows the raw p-values from hypothesis testing for group differences as color-maps on mean shapes of the autism group (top row) and the normal control group (bottom row). Red indicates areas where significant group differences were found (p-values $< 0.05$), with blue elsewhere (p-values$>= 0.05$). The top row shows the results when relative geometric scale is included, and the bottom shows relative scale removed. Structures are shown in the their mean orientations, positions, and scale in the global coordinate frame. We computed the average orientation for each structure using methods for averaging in | ||
| + | curved spaces. | ||
| + | |||
| + | [[Image:meanviews.png|thumbnail|Figure 3]] | ||
| + | |||
== Publications == | == Publications == | ||
* J. Cates, P. Thomas Fletcher, M. Styner, M. Shenton, R. Whitaker. Shape Modeling and Analysis with Entropy-Based Particle Systems. IPMI 2007, accepted. | * J. Cates, P. Thomas Fletcher, M. Styner, M. Shenton, R. Whitaker. Shape Modeling and Analysis with Entropy-Based Particle Systems. IPMI 2007, accepted. | ||
* J. Cates, P. Thomas Fletcher, R. Whitaker. Entropy-Based Particle Systems for Shape Corresopndence. Mathematical Foundations of Computational Anatomy Workshop, MICCAI 2006. pp. 90-99 Oct 2006. | * J. Cates, P. Thomas Fletcher, R. Whitaker. Entropy-Based Particle Systems for Shape Corresopndence. Mathematical Foundations of Computational Anatomy Workshop, MICCAI 2006. pp. 90-99 Oct 2006. | ||
Revision as of 17:19, 19 April 2007
Home < Algorithm:UtahContents
DTI Processing and Analysis
- Differential Geometry. We will provide methods for computing geodesics and distances between diffusion tensors. Several different metrics will be made available, including a simple linear metric and also a symmetric space (curved) metric. These routines are the building blocks for the routines below.
- Statistics Given a collection of diffusion tensors, compute the average and covariance statistics. This can be done using the metrics and geometry routines above. A general method for testing differences between groups is planned. The hypothesis test also depends on the underlying geometry used.
- Interpolation Interpolation routines will be implemented as a weighted averaging of diffusion tensors in the metric framework. The metric may be chosen so that the interpolation preserves desired properties of the tensors, e.g., orientation, size, etc.
- Filtering We will provide anisotropic filtering of DTI using the full tensor data (as opposed to component-wise filtering). Filtering will also be able to use the different metrics, allowing control over what properties of the tensors are preserved in the smoothing. We have also developed methods for filtering the original diffusion weighted images (DWIs) that takes the Rician distribution of MR noise into account (see MICCAI 2006 paper below).
Volumetric White Matter Connectivity
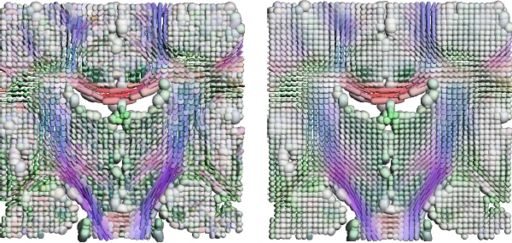
We have developed a PDE-based approach to white matter connectivity from DTI that is founded on the principal of minimal paths through the tensor volume. Our method computes a volumetric representation of a white matter tract given two endpoint regions. We have also developed statistical methods for quantifying the full tensor data along these pathways, which should be useful in clinical studies using DT-MRI. This work has been accepted to IPMI 2007.
- Relation to other NA-MIC projects:
- DTI processing: filtering and interpolation are an input to further analysis, such as UNC fiber tract analysis and MGH atlas building.
- DTI statistics: (UNC) will be used in the analysis of tensor data along fiber tracts.
Publications
- Fletcher, P.T., Tao, R., Jeong, W.-K., Whitaker R.T., "A Volumetric Approach to Quantifying Region-to-Region White Matter Connectivity in Diffusion Tensor MRI," to appear Information Processing in Medical Imaging (IPMI) 2007.
- Basu, S., Fletcher, P.T., Whitaker, R., "Rician Noise Removal in Diffusion Tensor MRI," presented at Medical Image Computing and Computer-Assisted Intervention, MICCAI 2006, LNCS 4190, pp. 117--125. PDF of paper
- Corouge, I., Fletcher, P.T., Joshi, S., Gilmore, J.H., and Gerig, G., "Fiber Tract-Oriented Statistics for Quantitative Diffusion Tensor MRI Analysis," Medical Image Analysis 10 (2006), 786--798.
- Corouge, I., Fletcher, P.T., Joshi, S., Gilmore J.H., and Gerig, G., "Fiber Tract-Oriented Statistics for Quantitative Diffusion Tensor MRI Analysis," in Proceedings of Medical Image Computing and Computer-Assisted Intervention (MICCAI 2005), LNCS 3749, pp. 131--138.
Activities
- Developed a Slicer module for our DT-MRI Rician noise removal during the 2007 Project Half Week. Also enhanced the method by including an automatic method for determining the noise sigma in the image.
- Developed prototype of DTI geometry package. This includes an abstract class for computing distances and geodesics between tensors, while derived classes can specify the particular metric to use. Current implemented subclasses are the basic linear metric and the symmetric space metric.
- Developed prototype of DTI statistical package. A general class has been developed for computing averages and principal modes of variation of tensor data. The statistics class can use any of the metrics described above.
- We have begun work on a general method for hypothesis testing of differences in two diffusion tensor groups. This method works on the full six-dimensional tensor information, rather than derived measures. The hypothesis testing class can also use any of the different tensor metrics.
- Participated in the Programmer's Week (June 2005, Boston). During this week the DTI statistics code was developed and added to the NA-MIC toolkit. See our Progress Report (July 2005). We are also involved in the Statistical Feature Analysis Framework project with Martin Styner (UNC) and Jim Miller (GE).
Software
The diffusion tensor statistics code is now part of the NA-MIC toolkit. To get the code, check out the NA-MIC SandBox (see instructions here) -- our code is in the "DiffusionTensorStatistics" directory.
MRI Segmentation
- We have implemented the MRI Tissue Classification Algorithm described in [1]. Classes for non-parametric density estimation and automatic parameter selection have been implemented as the basic framework on which we build the classification algorithm.
- The stochastic non-parametric density estimation framework is very general and allows the user to change kernel types (we have coded isotropic Gaussian, but additional kernels can easily be derived from the same parent class) and sampler types (for example local vs. global image sampling as well as sampling in non-image data) as template parameters.
- The classification class uses the stochastic non-parametric density estimation framework to implement the algorithm in [1].
- An existing ITK bias correction method has been incorporated into the method.
- Currently, we are registering atlas images to our data using the stand-alone LandmarkInitializedMutualInformationRegistration application. Ideally, we'd like to incorporate an exiting registration algorithm into our code so that classification can be carried out in one step. The initialization to the registration can be provided as command line arguments.
Publications
- Tolga Tasdizen, Suyash Awate, Ross Whitaker and Norman Foster, "MRI Tissue Classification with Neighborhood Statistics: A Nonparametric, Entropy-Minimizing Approach," Proceedings of MICCAI'05, Vol 2, pp. 517-525
Shape Modeling and Analysis
This research is a new method for constructing compact statistical point-based models of ensembles of similar shapes that does not rely on any specific surface parameterization. The method requires very little preprocessing or parameter tuning, and is applicable to a wider range of problems than existing methods, including nonmanifold surfaces and objects of arbitrary topology. The proposed method is to construct a point-based sampling of the shape ensemble that simultaneously maximizes both the geometric accuracy and the statistical simplicity of the model. Surface point samples, which also define the shape-to-shape correspondences, are modeled as sets of dynamic particles that are constrained to lie on a set of implicit surfaces. Sample positions are optimized by gradient descent on an energy function that balances the negative entropy of the distribution on each shape with the positive entropy of the ensemble of shapes. We also extend the method with a curvature-adaptive sampling strategy in order to better approximate the geometry of the objects. We have developed code based on ITK for computation of correspondence-based models, and have validated out method in several papers against several synthetic and real examples in two and three dimensions, including application to the statistical shape analysis of brain structures. We used hippocampus data from a schizo-typal personality disorder (SPD) study funded by the Stanley Foundation and UNC-MHNCRC (MH33127), and caudate data from a schizophrenia study funded by NIMH R01 MH 50740 (Shenton), NIH K05 MH 01110 (Shenton), NIMH R01 MH 52807 (McCarley), and a VA Merit Award (Shenton).
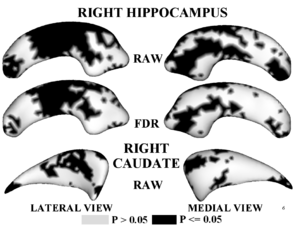
Figure 1,2 illustrates results of hypothesis testing for group differences from the control population for the left/right hippocampus and the left/right caudate. Raw and FDR-corrected p-values are given. Areas of significant group differences ($p <= 0.05$) are shown as dark regions. Areas with insignificant group differences ($p > 0.05$) are shown as light regions. Our results correlate with with other published hypothesis testing results on this data.
Our most recent work is in the application of the particle method to multi-object shape complexes. We have developed a novel method for computing surface point correspondences of multi-object anatomy that is a straightforward extension of the particle method for single-object anatomy. The correspondences take advantage of the statistical structure of an ensemble of complexes, and thus they are suitable for joint statistical analyses of shape and relative pose. The proposed method uses a dynamic particle system to optimize correspondence point positions across all structures in a complex simultaneously, in order to create a compact model of ensemble statistics. It is a different approach from previous methods for dealing with shape complexes, because to date researchers have considered the correspondence problem only for each structure independently, and have ignored intermodel correlations in the shape parameterization. These correlations are particularly important when the correspondences are constructed in order to reduce or minimize the information content of the ensemble.
We have developed a formulation of the multi-object correspondence optimization, and have applied it to a proof-of-concept application to the analysis of brain structure complexes from a longitudinal study of pediatric autism that is underway at UNC chapel hill. This work is in conjunction with Martin Styner, Heather Cody Hazlett, and Joe Piven. Figure 3 shows the raw p-values from hypothesis testing for group differences as color-maps on mean shapes of the autism group (top row) and the normal control group (bottom row). Red indicates areas where significant group differences were found (p-values $< 0.05$), with blue elsewhere (p-values$>= 0.05$). The top row shows the results when relative geometric scale is included, and the bottom shows relative scale removed. Structures are shown in the their mean orientations, positions, and scale in the global coordinate frame. We computed the average orientation for each structure using methods for averaging in curved spaces.
Publications
- J. Cates, P. Thomas Fletcher, M. Styner, M. Shenton, R. Whitaker. Shape Modeling and Analysis with Entropy-Based Particle Systems. IPMI 2007, accepted.
- J. Cates, P. Thomas Fletcher, R. Whitaker. Entropy-Based Particle Systems for Shape Corresopndence. Mathematical Foundations of Computational Anatomy Workshop, MICCAI 2006. pp. 90-99 Oct 2006.